An introduction to the theory of Spectral Submanifolds
Contents
First order dynamical systems
We consider dynamical systems of the form
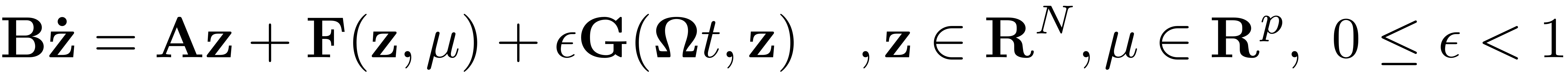
Any first order ODE (ordinary differential equation) and DAE
(differential algebraic equation) with smooth right hand side can be
brought to this standard form around its fixed points. After an
initial translation to set a fixed point to the origin of the
coordinate system, the right hand side can be rewritten to yield the
desired form. Here
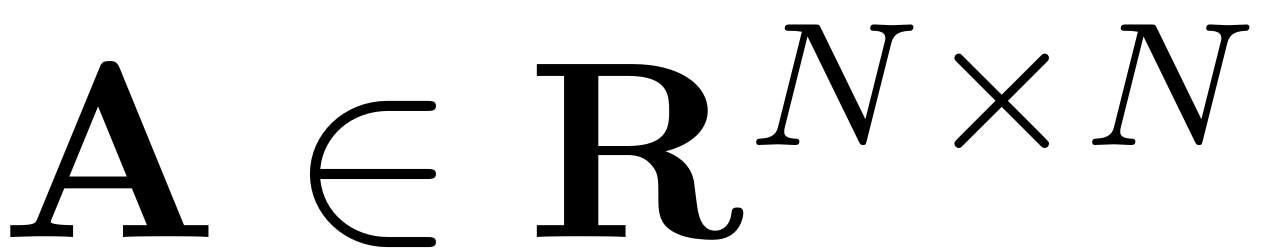 is the linear part of the dynamical system. Throughout the dynamical
systems literature the matrix
is the linear part of the dynamical system. Throughout the dynamical
systems literature the matrix
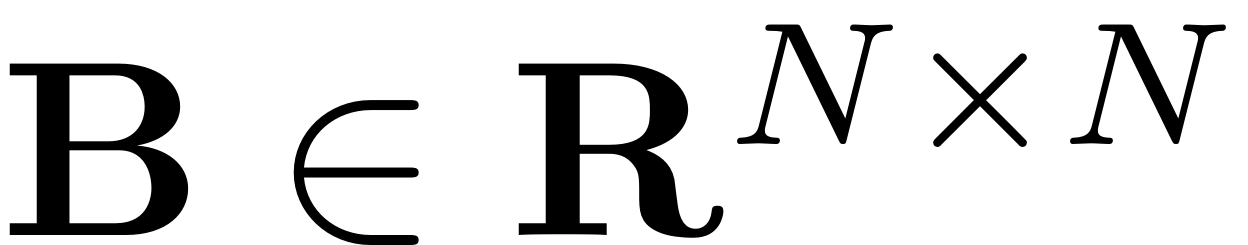 is often taken to be the identity. We do not make this assumption
and treat the general case, which leads to computational advantages
for dynamical systems that stem from second order ODEs as the
inversion of possibly large system matrices can be avoided this way,
and constrained mechanical systems in DAE formulations with Lagrange
multipliers, resulting in a singular matrix for B.
is often taken to be the identity. We do not make this assumption
and treat the general case, which leads to computational advantages
for dynamical systems that stem from second order ODEs as the
inversion of possibly large system matrices can be avoided this way,
and constrained mechanical systems in DAE formulations with Lagrange
multipliers, resulting in a singular matrix for B.
 is a vector valued nonlinear function and assumed to be
is a vector valued nonlinear function and assumed to be
 -times continuously differentiable in
-times continuously differentiable in
 and a set of parameters
and a set of parameters
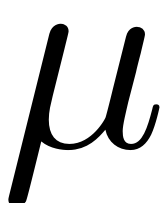 .
.
 is a non-autonomous and possibly non-linear function which contains
the time-dependent forcing that is acting on the system. This
forcing may for instance include direct, parametric, gyroscopic or
velocity-dependent terms.
is a non-autonomous and possibly non-linear function which contains
the time-dependent forcing that is acting on the system. This
forcing may for instance include direct, parametric, gyroscopic or
velocity-dependent terms.
Second order mechanical systems
Invariant manifolds such as SSMs can also be computed in the phase space of second order mechanical systems. These look as follows
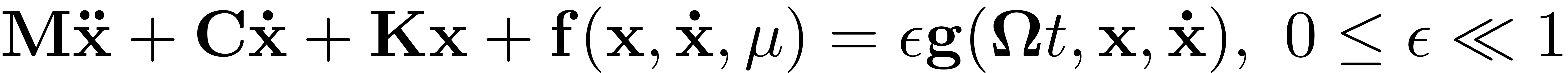
The linear part of the system is characterised by
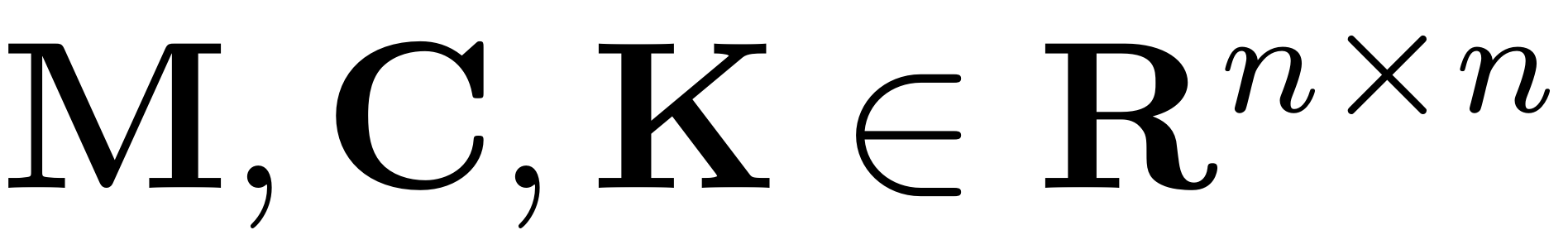 which denote the mass, damping and stiffness matrices, respectively.
The function
which denote the mass, damping and stiffness matrices, respectively.
The function
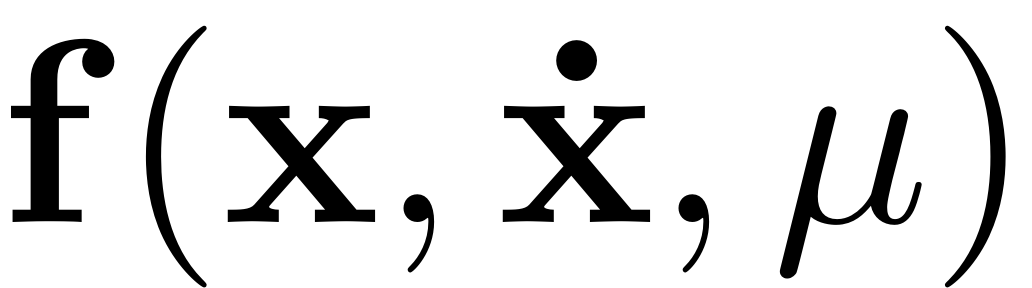 is a nonlinear function that is
is a nonlinear function that is
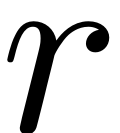 times continuously differentiable with
times continuously differentiable with
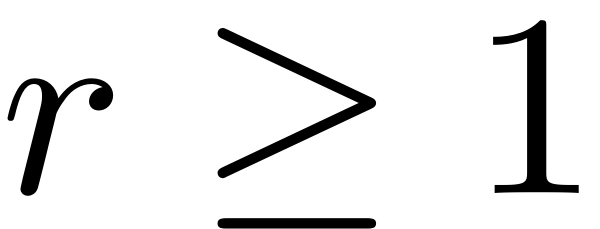 .The distinct types of time-dependent forces are represented by
general forcing vector
.The distinct types of time-dependent forces are represented by
general forcing vector
 . The second order form can be rewritten to the first order form,
for instance by choosing
. The second order form can be rewritten to the first order form,
for instance by choosing
![$$\mathbf{z} = \left[ \begin{array}{c} \mathbf{x} \\ \dot{\mathbf{x}} \end{array}
\right], \quad \mathbf{A} = \left[ \begin{array}{c} -\mathbf{K} \quad \mathbf{0}
\\ \mathbf{0} \quad \mathbf{M} \end{array} \right], \quad \mathbf{B} = \left[ \begin{array}{c}
\mathbf{C} \quad \mathbf{M} \\ \mathbf{M} \quad \mathbf{0} \end{array} \right], \quad
\mathbf{ F(z)} = \left[ \begin{array}{c}- \mathbf{f(x,\dot{x})} \\ \mathbf{0}
\end{array} \right], \quad \mathbf{ G}(\mathbf\Omega t, \mathbf{z}) = \left[
\begin{array} {c} \mathbf{g}(\mathbf\Omega t,\mathbf{x},\mathbf{\dot{x}}) \\
\mathbf{0}\end{array}\right]$$](SSM_Theory_eq01052373293453443383-Rescaled.png)
This choice to obtain the first-order form is not unique (cf. Jain & Haller, 2021) but all such forms can be used for the computation of SSMs. No assumption has to be made about the magnitude of the nonlinearities as the results presented here are valid for nonlinearities of any magnitude, the curvature of the computed manifolds depends smoothly on the magnitude of the nonlinearities.
Linear Part of the System
It is necessary to make an assumption on the spectrum of the two
constant matrices
 and
and
 . Consider the linear part of the dynamical system which is given as
. Consider the linear part of the dynamical system which is given as
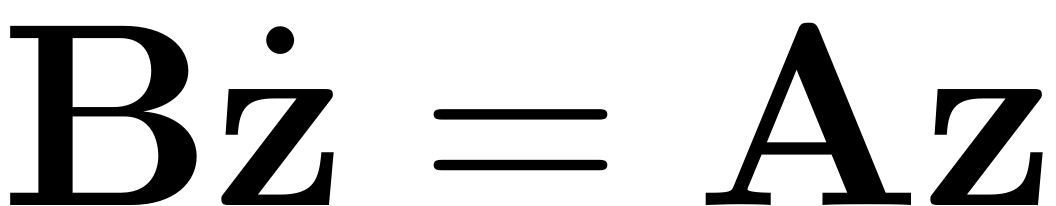
We assume that the two matrices are simultaneously diagonalisable,
that is, there exist
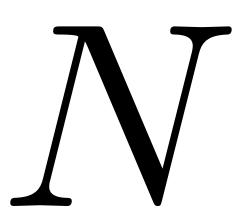 eigenvalues and left as well as right eigenvector pairs. In contrast
to the full spectrum, small subsets of eigenvalues and their
corresponding generalised eigenvectors can be computed efficiently
even for large systems (cf.
Golub & van Loan, 1996). We thus consider a subset of
eigenvalues and left as well as right eigenvector pairs. In contrast
to the full spectrum, small subsets of eigenvalues and their
corresponding generalised eigenvectors can be computed efficiently
even for large systems (cf.
Golub & van Loan, 1996). We thus consider a subset of
 eigenvalues given as
eigenvalues given as
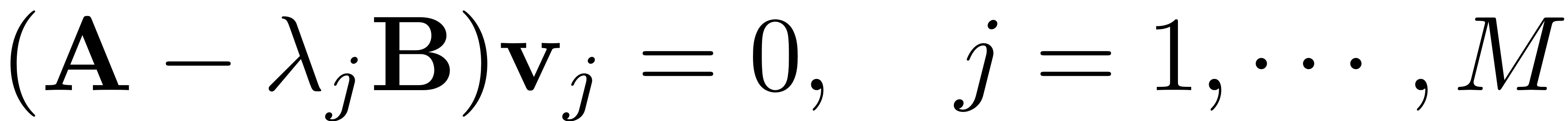
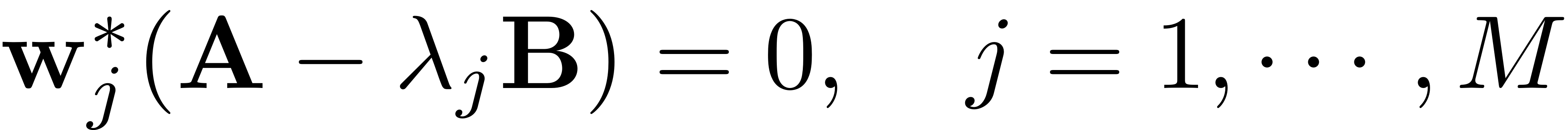
We arrange these eigenvectors in the increasing order of magnitudes of the real parts of the associated eigenvalues, i.e.,
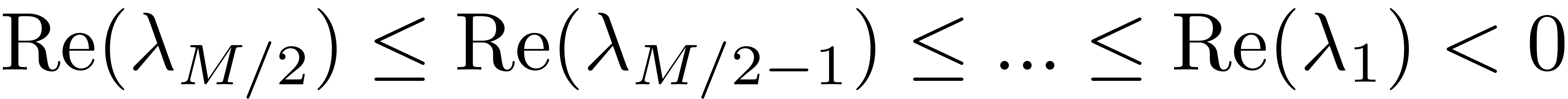
Note that the above procedure is valid for any general damping
matrix
 and reduces to the computation of the conservative eigenmodes when
and reduces to the computation of the conservative eigenmodes when
 is simultaneously diagonalisable with the mass and stiffness
matrices, e.g., in the case of proportional damping.
is simultaneously diagonalisable with the mass and stiffness
matrices, e.g., in the case of proportional damping.
The one-dimensional vector spaces that correspond to the span of the
eigenvectors are invariant under the linear part of the dynamics.
The reduced model associated to the chosen linear subspace
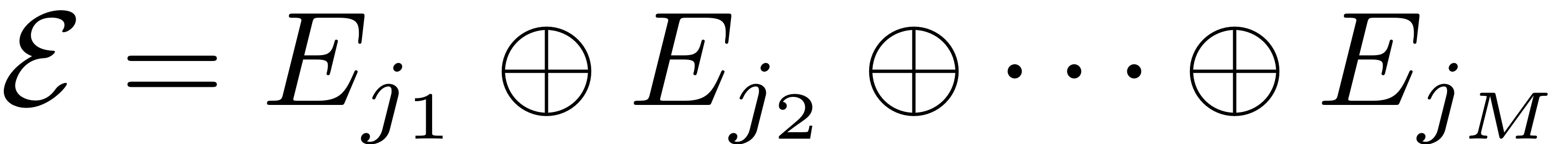 via projection of the linear system is thus exact. This subspace is
often called the master spectral subspace on which the linear
part of the full dynamics can be analysed. The eigenvalues in the
spectrum of the master subspace, denoted as
via projection of the linear system is thus exact. This subspace is
often called the master spectral subspace on which the linear
part of the full dynamics can be analysed. The eigenvalues in the
spectrum of the master subspace, denoted as
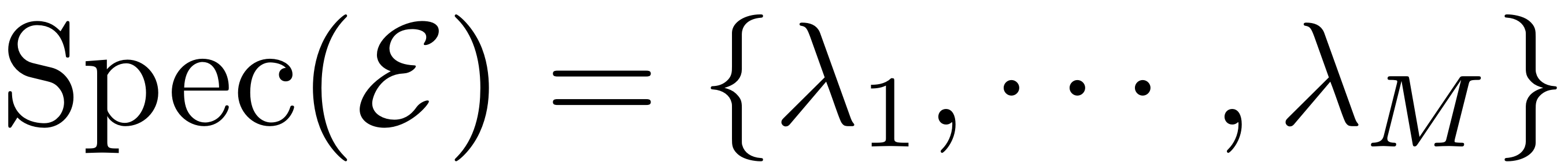 , are collected in the vector
, are collected in the vector
 . The master-eigenvectors are normalised such that
. The master-eigenvectors are normalised such that
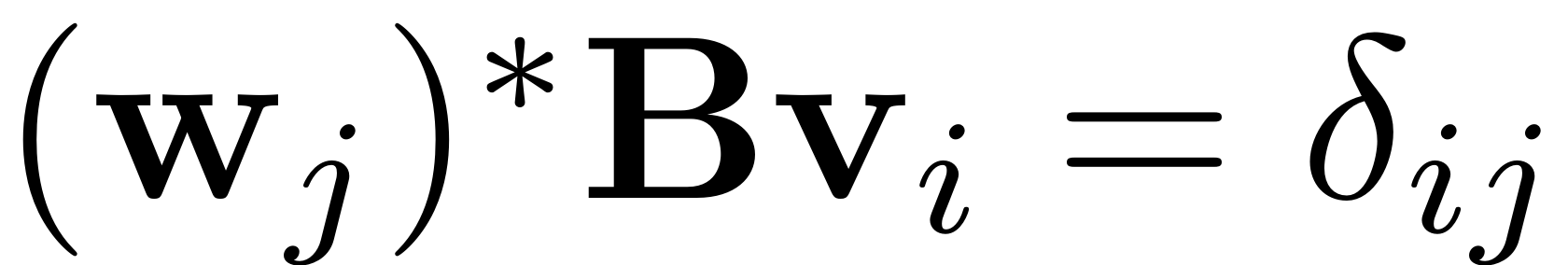 .
.
For the case of DAEs, the matrix B is singular, resulting in eigenvalues with infinite magnitude and eigenvectors corresponding to constraint modes. Moreover, when handling non-polynomial nonlinearities via DAEs in polynomial form, the linear system may admit zero eigenvalues. These eigenvalues with zero or infinite magnitude should not be included into the master subspace for model reduction.
Existence and computation of SSMs
When adding nonlinearities, the flat invariant subspace
 does not remain invariant. Model reduction onto this subspace
thus should not be performed anymore as trajectories within this
subspace do not correspond to full system trajectories. A linear
projection may kill essential nonlinear couplings and thus predict
wrong behaviour of the reduced system even on a qualitative level,
including the emergence of non-physical fixed points - we illustrate
this phenomenon in a small
example. This is where the computation of nonlinear invariant manifolds
becomes relevant. As these manifolds are invariant, properties of
the ROM such as periodic orbits and invariant tori as well as
bifurcations that are found are guaranteed to exist in the full
physical system. Encountering an invariant torus on an invariant
manifold thus directly implies that an invariant torus of the full
system has been found.
does not remain invariant. Model reduction onto this subspace
thus should not be performed anymore as trajectories within this
subspace do not correspond to full system trajectories. A linear
projection may kill essential nonlinear couplings and thus predict
wrong behaviour of the reduced system even on a qualitative level,
including the emergence of non-physical fixed points - we illustrate
this phenomenon in a small
example. This is where the computation of nonlinear invariant manifolds
becomes relevant. As these manifolds are invariant, properties of
the ROM such as periodic orbits and invariant tori as well as
bifurcations that are found are guaranteed to exist in the full
physical system. Encountering an invariant torus on an invariant
manifold thus directly implies that an invariant torus of the full
system has been found.
Spectral Submanifolds (SSMs) can be interpreted as the smoothest nonlinear (and non-autonomous) analogon of invariant spectral subspaces for nonlinear systems. These nonlinear invariant manifolds are tangent to given spectral subspaces and perturb smoothly from them in the magnitude of the nonlinearity. The dynamics on an SSM is called the reduced dynamics and due to the invariance of the SSM serves as an exact reduced order model (ROM) of the full system. The existence of SSMs rests on a set of non-resonance conditions, as any resonance between two modes will disallow their separation when computing the respective invariant manifolds. Details on the handling of systems with resonances can be found here and in Li et al., 2022 Li & Haller 2022. The degree of smoothness at which SSMs become unique is also coupled to the spectrum of the linear part of the dynamical system, more details on this are provided here and in Haller & Ponsioen, 2016, Ponsioen Pedergnana & Haller, 2018.
Before we proceed to compute such invariant manifolds and use them for model reduction, however, it is essential to guarantee that the objects that we are looking for, do really exist. Haller & Ponsioen, 2016 establish the existence and uniqueness of SSMs under certain non-resonance conditions. Before computing an SSM, these conditions have to be checked, to guarantee that the SSM exists. If its existence is not guaranteed, then it is also not guaranteed that the computed ROM lives in an invariant manifold of the full physical space and model reduction to this ROM looses its mathematical justification.
Autonomous SSM
Consider the
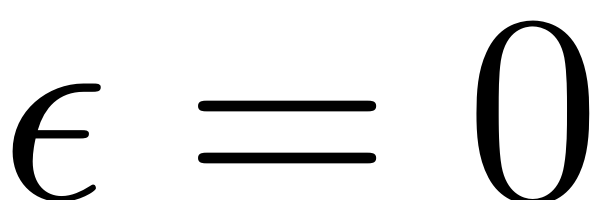 limit of the dynamical system, ie. the autonomous case. We define
the relative spectral quotient as
limit of the dynamical system, ie. the autonomous case. We define
the relative spectral quotient as
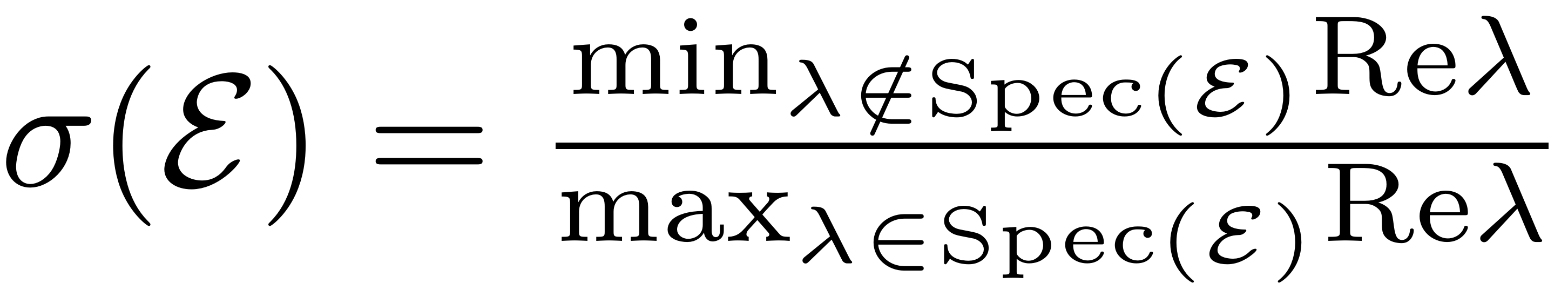
It is the relation of the smallest real part of an eigenvalue
outside the master subspace to the eigenvalue in the subspace with
largest real part. More details on the interpretation of this
coefficient are provided in
Resonances.
Formally the existence of autonomous SSMs attached to a fixed point
and tangent to a spectral subspace
 of an autonomous dynamical system is guaranteed by the following
theorem (Haller & Ponsioen, 2016).
of an autonomous dynamical system is guaranteed by the following
theorem (Haller & Ponsioen, 2016).
Theorem (Autonomous SSM)
For all
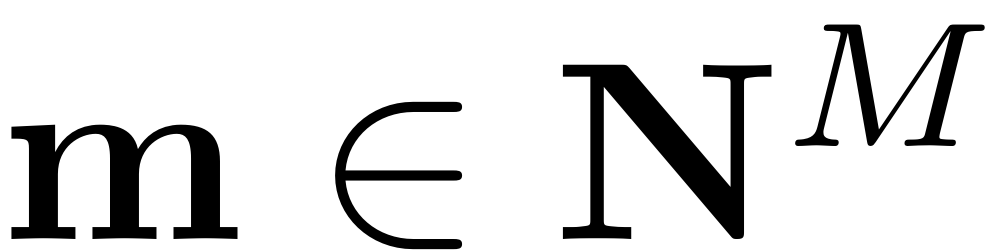 with
with
 assume the non-resonance conditions
assume the non-resonance conditions
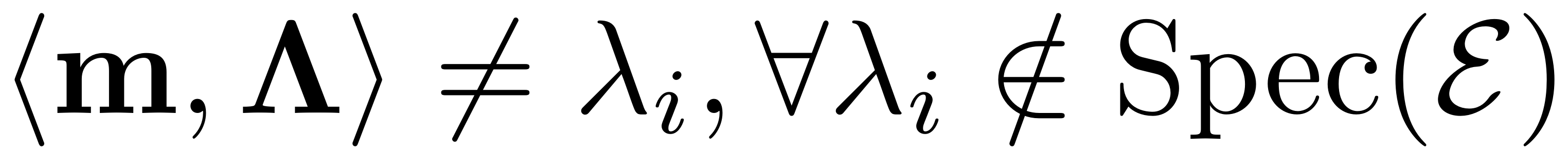
that is, for all eigenvalues
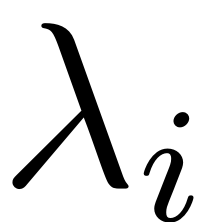 that lie outside the spectrum of
that lie outside the spectrum of
 . Then the following statements hold
. Then the following statements hold
-
There exists a class
 SSM,
SSM,
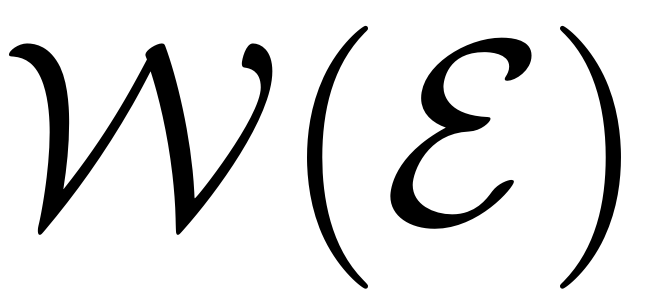 , tangent to
, tangent to
 at the trivial equilibrium point
at the trivial equilibrium point
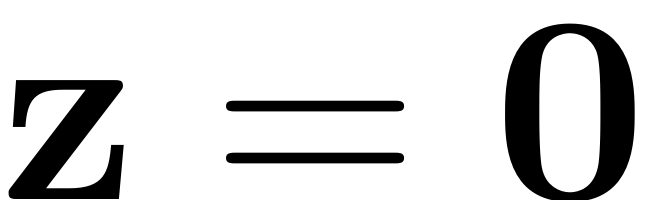 . Furthermore
. Furthermore
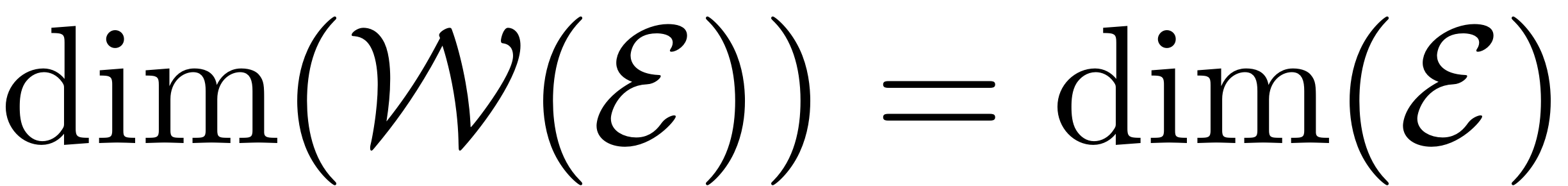 .
.
-
 is unique among all
is unique among all
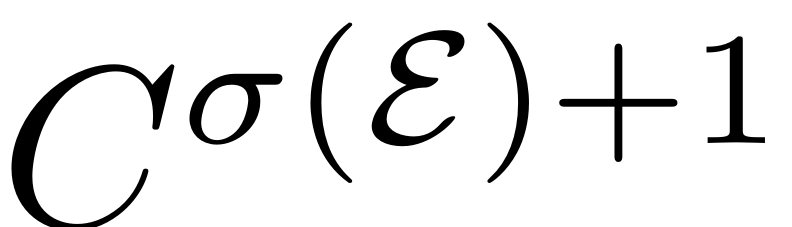 invariant manifolds with the properties listed in 1.
invariant manifolds with the properties listed in 1.
-
If
 is jointly
is jointly
 in
in
 and an additional parameter vector
and an additional parameter vector
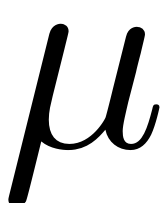 , then the SSM
, then the SSM
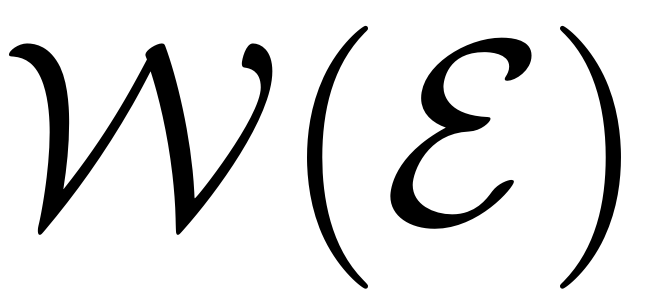 is also jointly
is also jointly
 in
in
 and
and
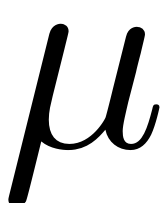 .
.
The third point guarantees the existence of the SSMs for arbitrary magnitudes of the nonlinearity. Therefore the technique presented here does not leverage on any assumption concerning the magnitude of the nonlinearity, such as eg. perturbation techniques.
The components orthogonal to the slowest SSM decay onto the manifold for all trajectories in a neighbourhood of the stable fixed point of interest. The parallel components synchronise with the reduced dynamics on the SSM, hence they constitute a predictive ROM for the full system. If transient response is of interest, then intermediate SSMs may be constructed to observe the system. As SSMs are invariant, any dynamics on them is also guarenteed to exist in the full system.
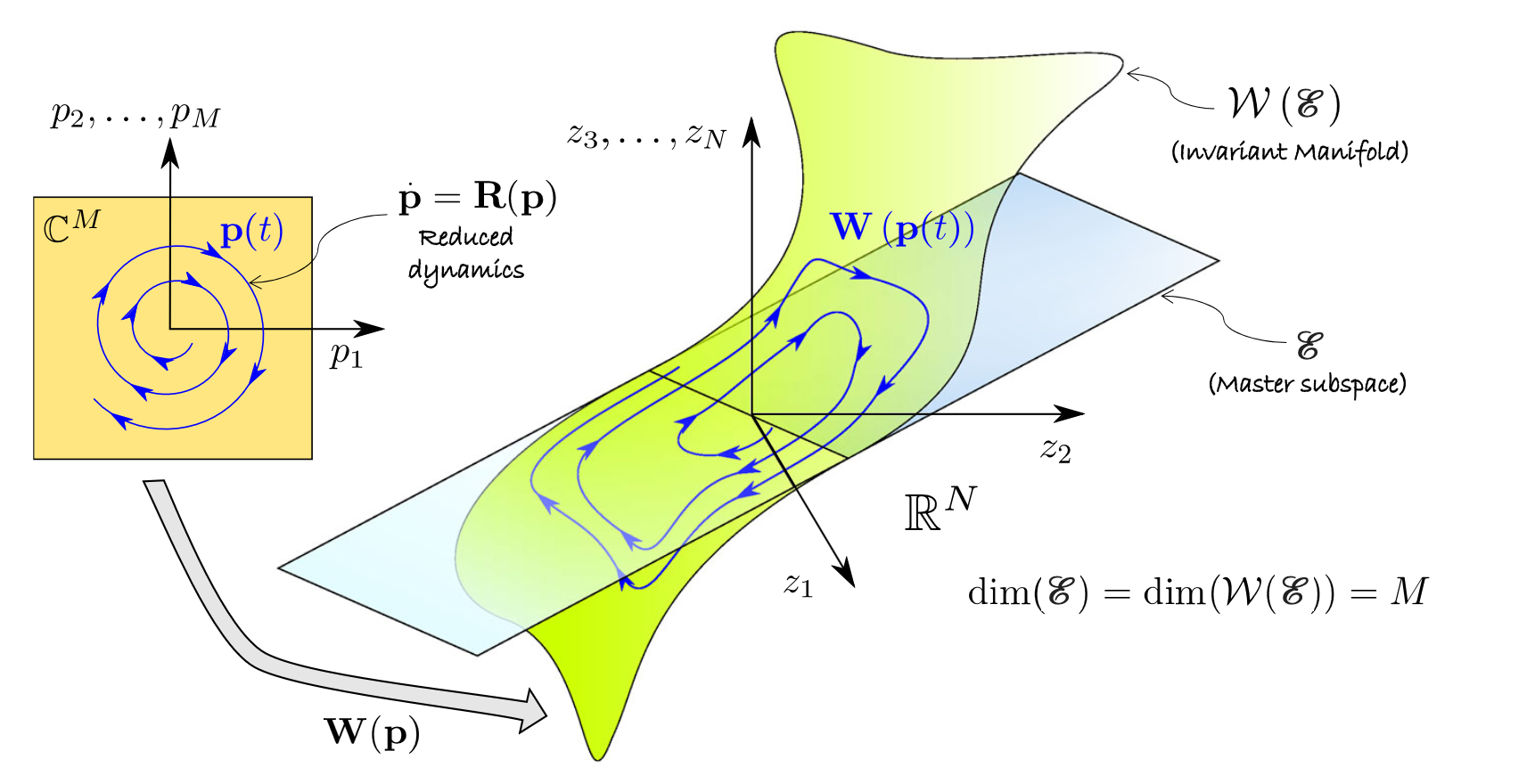
The following figure (cf.
Jain & Haller, 2021) depicts, how such an SSM is represented via a parametrisation. It
is given by a map
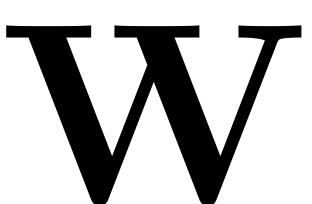 that maps the
that maps the
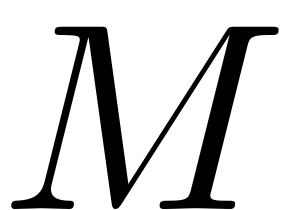 parametrisation coordinates onto a
parametrisation coordinates onto a
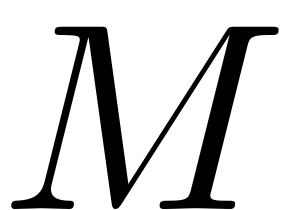 - dimensional manifold
- dimensional manifold
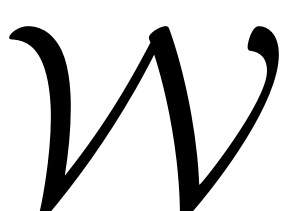 in full phase space. This manifold is tangent to the master spectral
subspace
in full phase space. This manifold is tangent to the master spectral
subspace
 . The reduced dynamics on the SSM are represented by
. The reduced dynamics on the SSM are represented by
 and constitute an exact ROM for the full system. Due to the
invariance, any trajectory of the reduced dynamics in the
parametrisation space is mapped onto a trajectory on
and constitute an exact ROM for the full system. Due to the
invariance, any trajectory of the reduced dynamics in the
parametrisation space is mapped onto a trajectory on
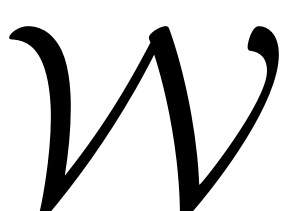 on the full phase space. For an explanation on the computation of
the SSM and the reduced dynamics see
Computation of SSMs. For
more explanations on the choice and importance of
on the full phase space. For an explanation on the computation of
the SSM and the reduced dynamics see
Computation of SSMs. For
more explanations on the choice and importance of
 refer to
Resonances.
refer to
Resonances.
Non-autonomous SSMs
The autonomous treatment of SSMs can be extended if the dynamical
system is driven via time dependent forcing terms. We consider
quasiperiodic (possibly parametric) excitation of the form
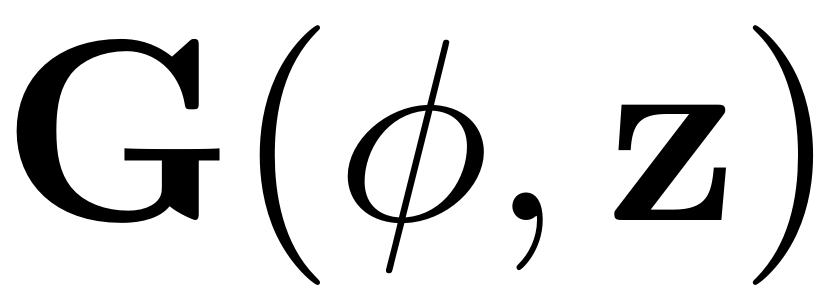 . The (quasi)-periodic phase variable
. The (quasi)-periodic phase variable
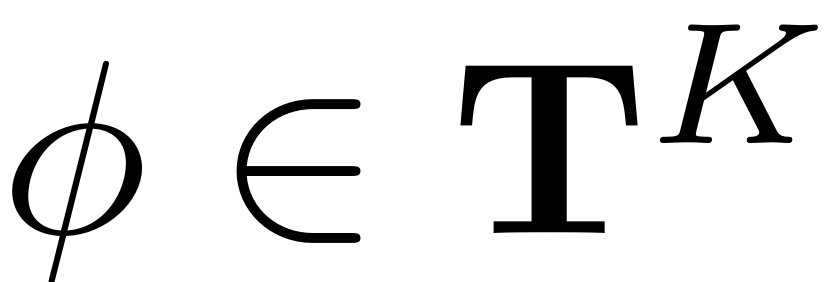 introduces time dependence via the dynamical set of equations
introduces time dependence via the dynamical set of equations
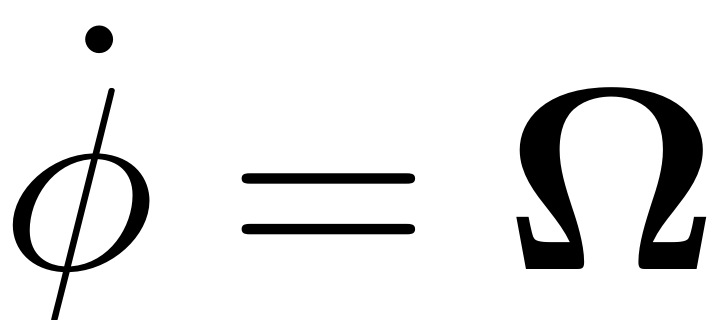 . The vector
. The vector
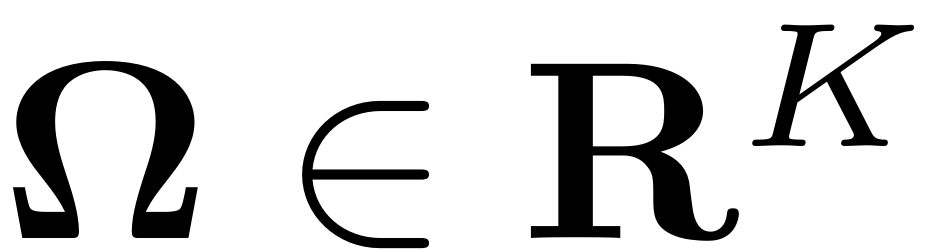 is the frequency vector and gives the basis of the quasiperiodic
excitation with
is the frequency vector and gives the basis of the quasiperiodic
excitation with
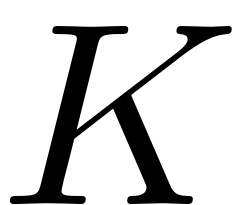 incommensurate frequencies. As a result the dynamical system reads
incommensurate frequencies. As a result the dynamical system reads
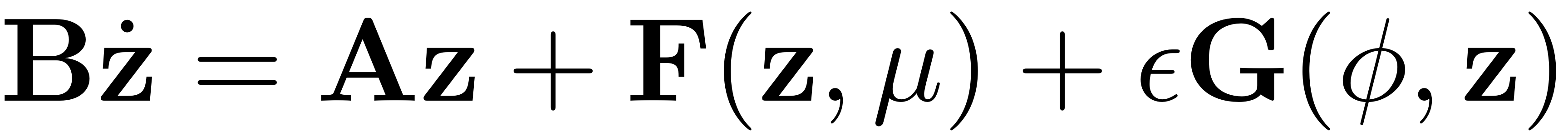
For small enough excitation amplitude the trivial fixed point of the
autonomous system perturbs smoothly into an invariant torus
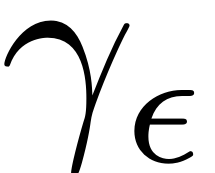 as
as
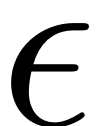 is increased (cf.
Guckenheimer & Holmes, 1983).
is increased (cf.
Guckenheimer & Holmes, 1983).
Instead of being attached to the trivial fixed point
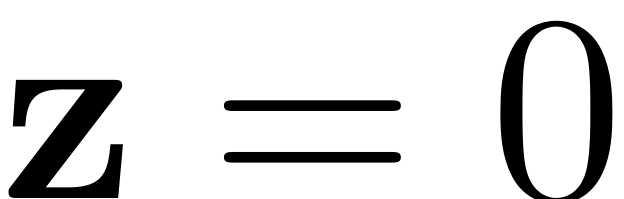 , the non-autonomous SSM sticks to the invariant Torus
, the non-autonomous SSM sticks to the invariant Torus
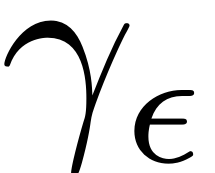 .
.
The SSM stays attached to this torus at its base and thus starts to
move in phase space in a quasiperiodic fashion. In mathematical
terms, the tangency to
 in the autonomous case implies that the non-autonomous SSM is
tangent to the spectral subbundle
in the autonomous case implies that the non-autonomous SSM is
tangent to the spectral subbundle
 . Furthermore the manifold also starts to deform quasiperiodically.
The existence of the non-autonomous SSM builds on non-resonance
conditions similar to the autonomous manifold. The absolute spectral
quotient which determines the degree of smoothness, beyond which the
SSM is unique, is defined as
. Furthermore the manifold also starts to deform quasiperiodically.
The existence of the non-autonomous SSM builds on non-resonance
conditions similar to the autonomous manifold. The absolute spectral
quotient which determines the degree of smoothness, beyond which the
SSM is unique, is defined as
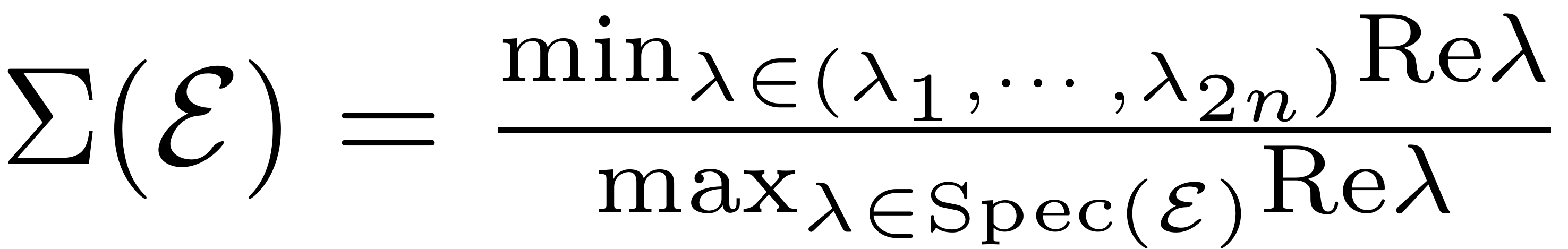
It differs from the relative quotient insofar that it includes the minimum over the full eigenvalue spectrum, also including the eigenvalues which are in the master spectrum. Commonly the slowest modes are of interest in practical applications. These tend to show the weakest dissipative behaviour and thus have eigenvalues with the lowest real part. Hence uniqueness of the non-autonomous manifold for those SSMs sets in at possibly higher orders than for the autonomous manifold. The existence and uniqueness of these non-autonomous manifolds in general is established in the succeeding theorem by Haller & Ponsioen, 2016.
Theorem (Non-autonomous SSM)
For all
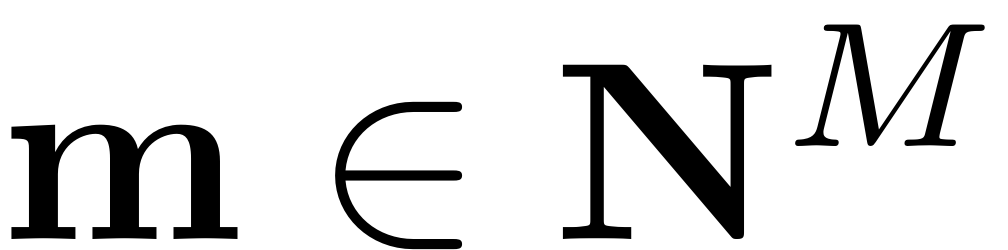 with
with
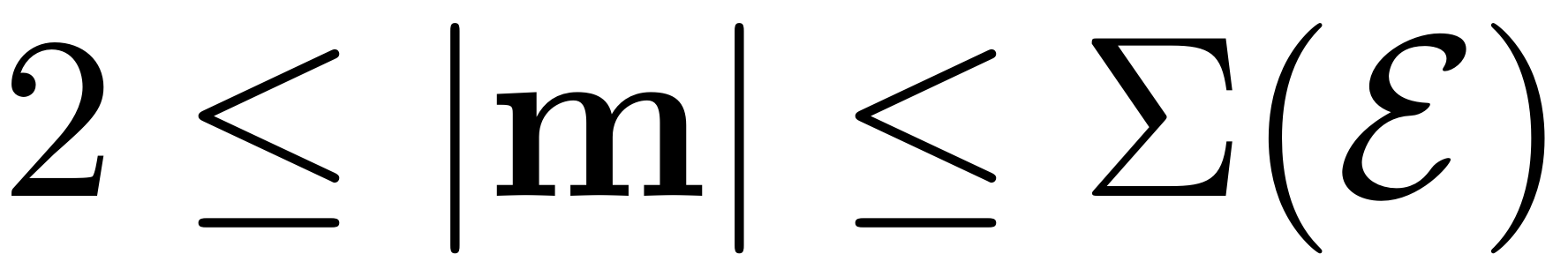 assume the non-resonance conditions
assume the non-resonance conditions
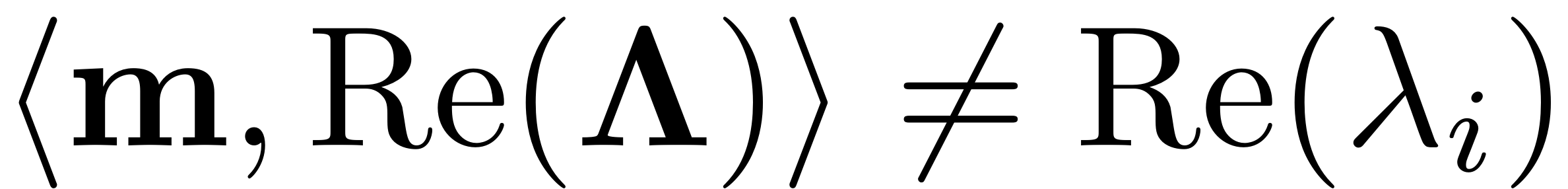
for all eigenvalues
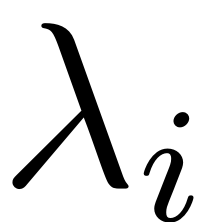 outside of the master subspace, so
outside of the master subspace, so
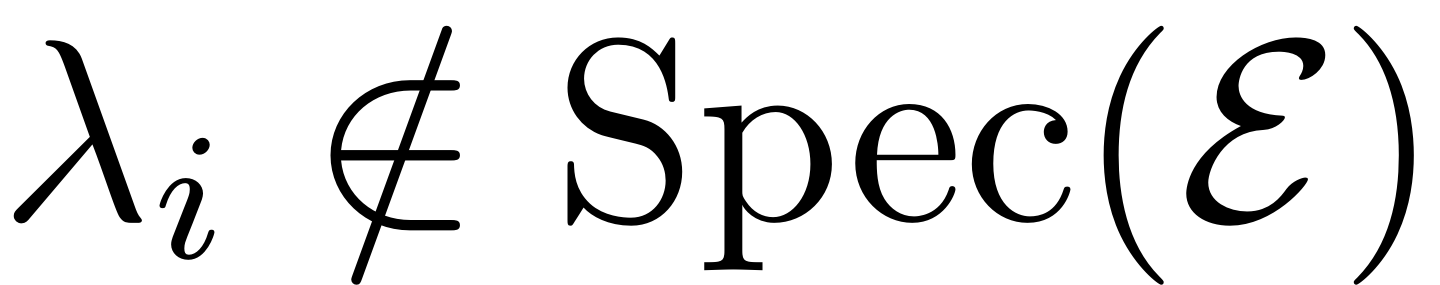 . Then the following is true
. Then the following is true
-
There exists a unique, quasiperiodic,
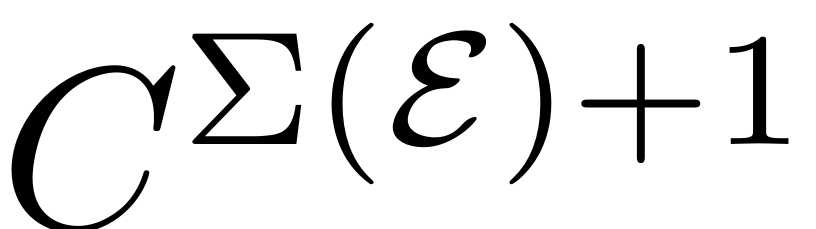 SSM,
SSM,
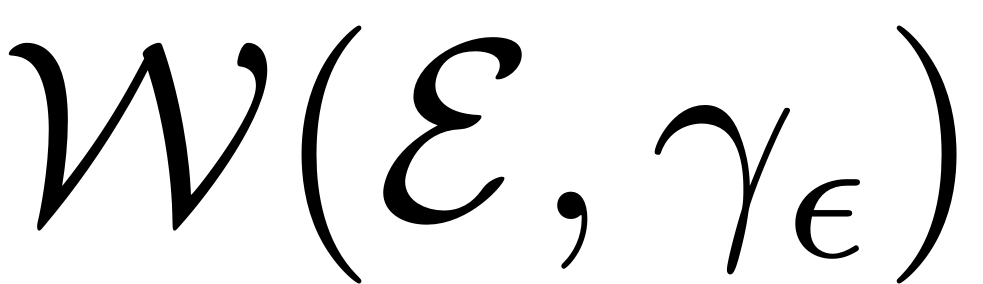 , which perturbs smoothly in
, which perturbs smoothly in
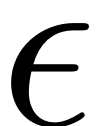 . Furthermore
. Furthermore
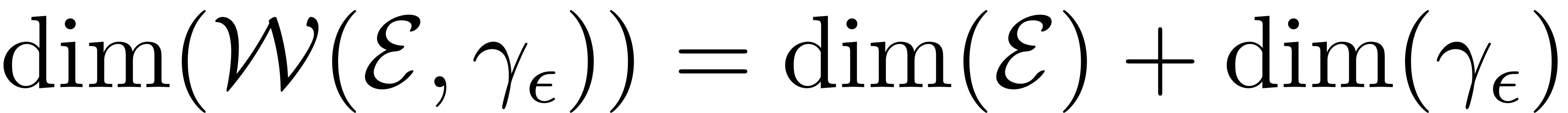 .
.
-
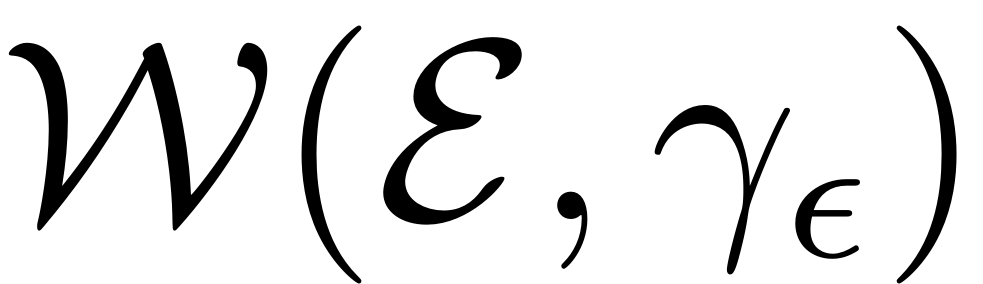 can be described by a parametrization
can be described by a parametrization
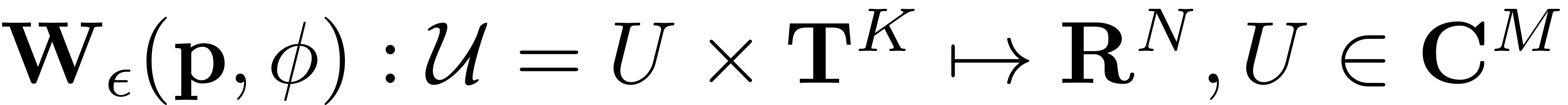 from an open set
from an open set
 onto the phase space of the full system.
onto the phase space of the full system.
-
There exists a vector field
 which satisfies the invariance equation
which satisfies the invariance equation
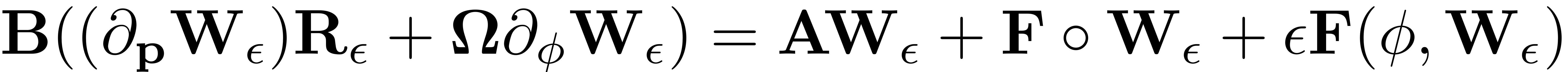 and gives the reduced dynamics on the SSM:
and gives the reduced dynamics on the SSM:
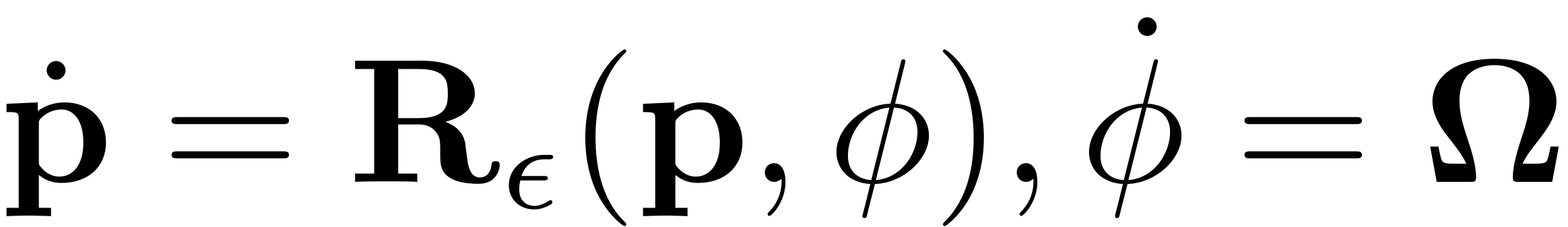
For the derivation of this invariance equation and further
mathematical details please refer to the
SSM-Computations page. It is
thus our task to compute a mathematical presentation of the manifold
parametrisation
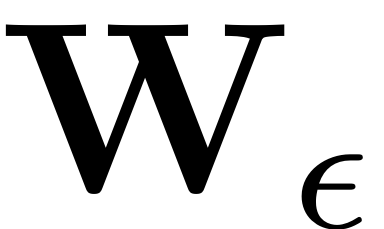 and the reduced dynamics
and the reduced dynamics
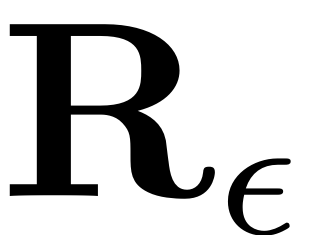 . Consequently these can then be used for further analysis, for
instance the computation of
backbone curves,
Forced Response Curves,
continuation of the reduced dynamics
or
stability diagrams.
. Consequently these can then be used for further analysis, for
instance the computation of
backbone curves,
Forced Response Curves,
continuation of the reduced dynamics
or
stability diagrams.
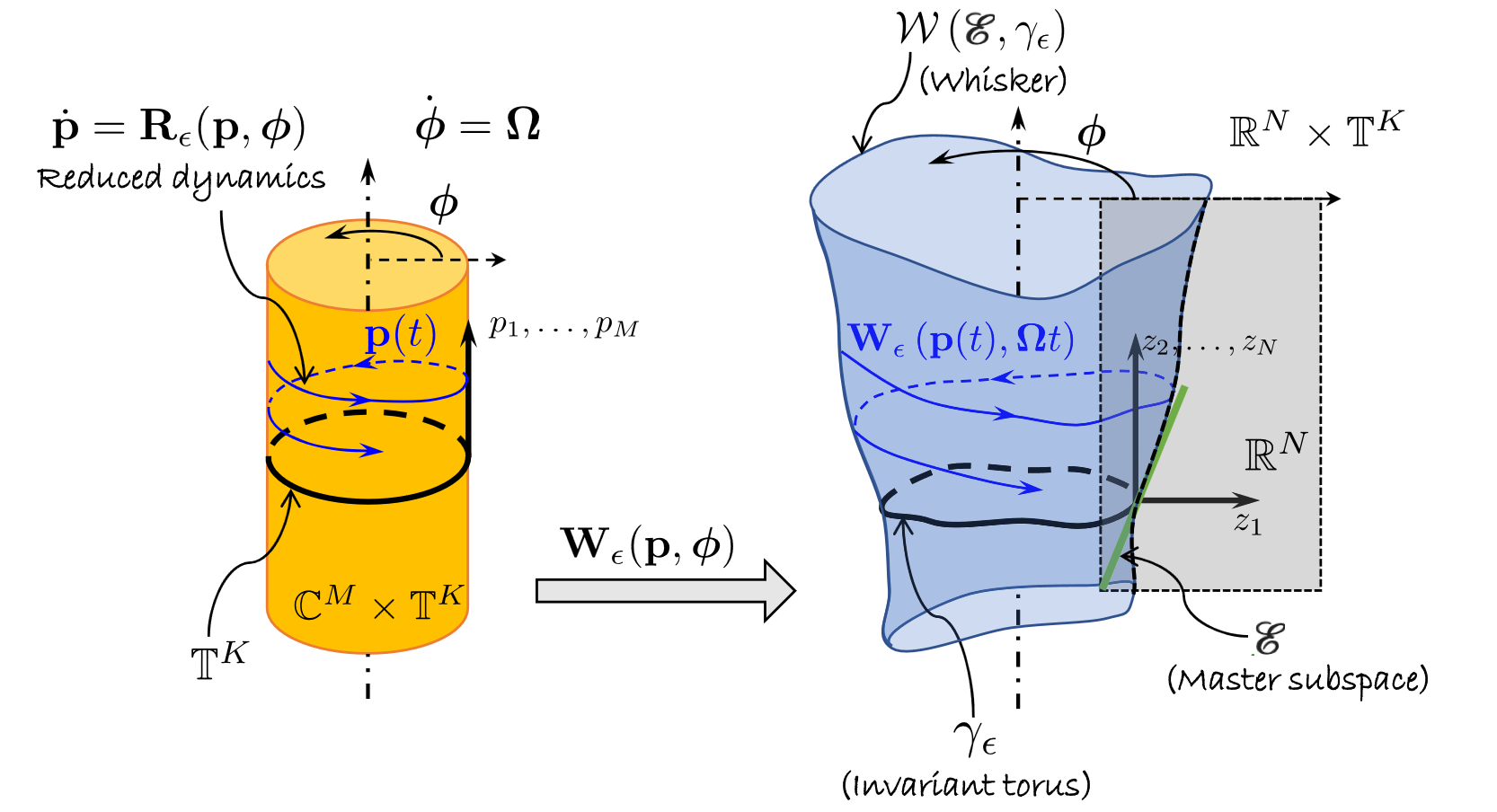
In the following figure (cf.
Jain & Haller, 2021), the parametrisation of such a non-autonomous SSM and the reduced
dynamics on it are visualised schematically. The parametrisation
space (yellow) consists of a direct product of
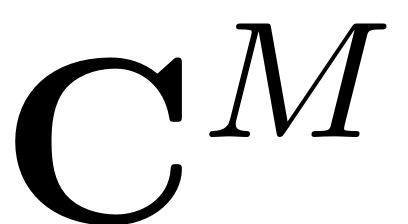 , which contains the spacial parametrisation coordinates, with the
, which contains the spacial parametrisation coordinates, with the
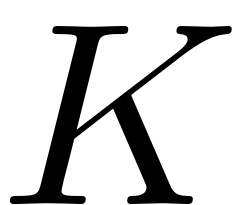 - dimensional torus
- dimensional torus
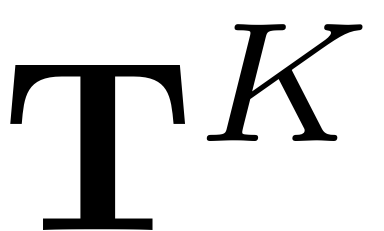 , which includes the temporal variables. The parametrisation
, which includes the temporal variables. The parametrisation
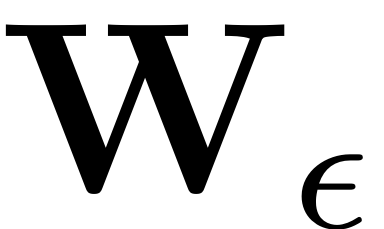 then maps this direct product onto the invariant, non-autonomous
manifold (blue) in the full, non-autonomous phase space. The spatial
euclidian coordinates of this phase space are represented with a
gray rectangle. At each instance in time, the non-autonomous SSM
then maps this direct product onto the invariant, non-autonomous
manifold (blue) in the full, non-autonomous phase space. The spatial
euclidian coordinates of this phase space are represented with a
gray rectangle. At each instance in time, the non-autonomous SSM
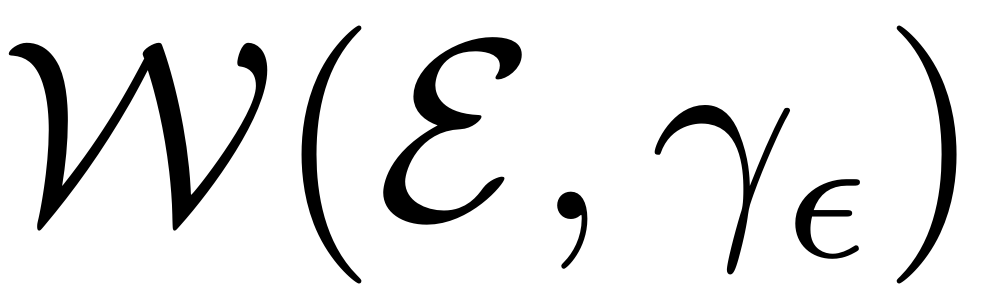 is tangent to the master subspace
is tangent to the master subspace
 (green). The temporal evolution of the manifold parametrisation
implies that, as time passes, the SSM stays tangent to the subbundle
(green). The temporal evolution of the manifold parametrisation
implies that, as time passes, the SSM stays tangent to the subbundle
 . The SSM furthermore deformes in a quasiperiodic manner, according
to the frequencies and harmonics present in the external excitation.
. The SSM furthermore deformes in a quasiperiodic manner, according
to the frequencies and harmonics present in the external excitation.
Unstable SSMs and fractional SSMs
The above SSM theory assumes that the fixed point is asymptotically stable. However, this theory can be easily extended to hyperbolic fixed point, where reduction on unstable and mix-mode SSMs becomes more relevant. In particular, the definition of spectral quotients will be changed. More details on this extension can be found in Cenedese et al., 2022. Recently, theories on fractional (secondary) SSMs Haller et al., 2023 and temporally aperiodic SSMs Haller and Kaundinya, 2024 were developed. These developments significantly enhance the applicability of SSMs.
