Computing backbone curves
Let us consider an autonomous dynamical mechanical system
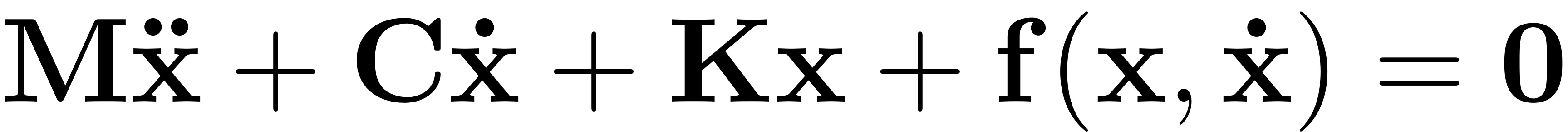
with nonlinear internal forces
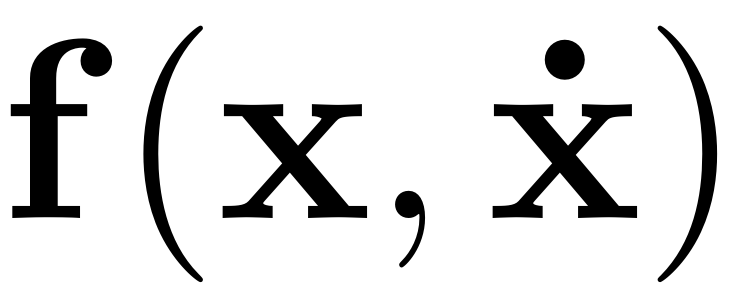 .
.
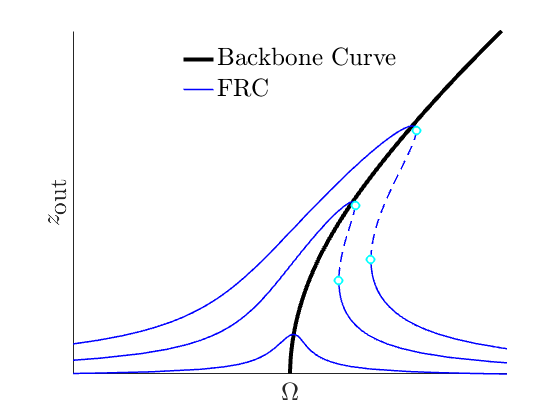
The backbone curve of such a system is defined as the collection of points which sit at the locus, ie. the point of maximal amplitude, of the nonlinear forced oscillations of a system. In this tutorial will motivate how such a curve can be obtained directly from the ROM provided by the reduced dynamics on a 2-dimensional SSM. In the following figure an illustration of a backbone curve is given, along with the forced response with various forcing amplitudes. Depending on the magnitude and characteristics of the nonlinear internal forces, the curve will bend in different ways, thus giving conclusive results about they system's nonlinear properties.
Contents
SSM Computation
Assume we are interested in the nonlinear behaviour of the
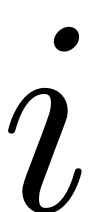 -th mode. Its linear response frequency is determined via the
eigenvalue problem
-th mode. Its linear response frequency is determined via the
eigenvalue problem
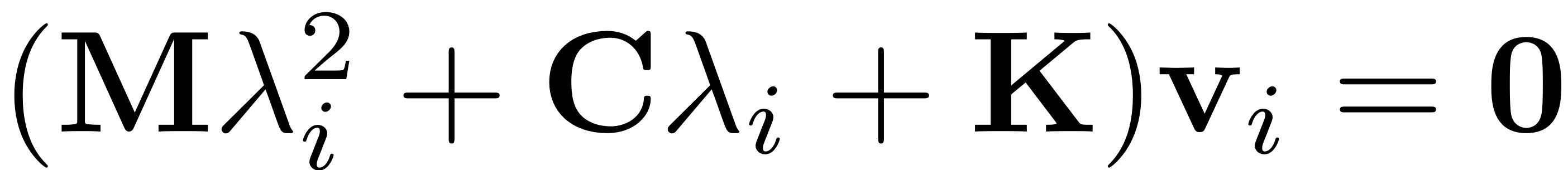
where the resonance frequency is
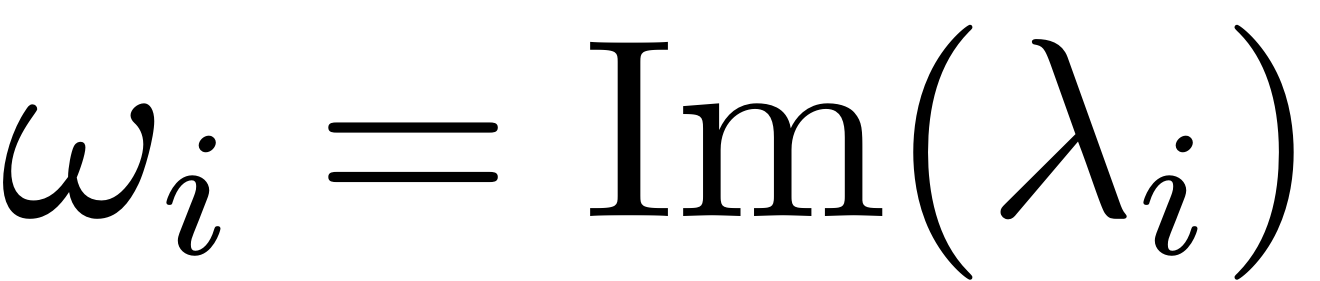 . Assume also that there are
no outer resonances and
procede with constructing a ROM on the autonomous SSM which is
computed as a nonlinear continuation of
. Assume also that there are
no outer resonances and
procede with constructing a ROM on the autonomous SSM which is
computed as a nonlinear continuation of
 . The following figure (cf. Jain & Haller, 2021) depicts how the
manifold is embedded in the full space via the autonomous
parametrisation
. The following figure (cf. Jain & Haller, 2021) depicts how the
manifold is embedded in the full space via the autonomous
parametrisation
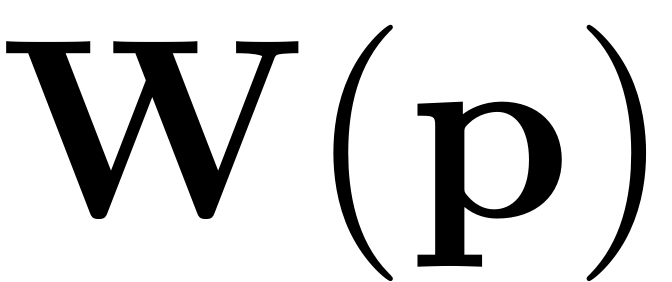 of the invariant SSM.
of the invariant SSM.
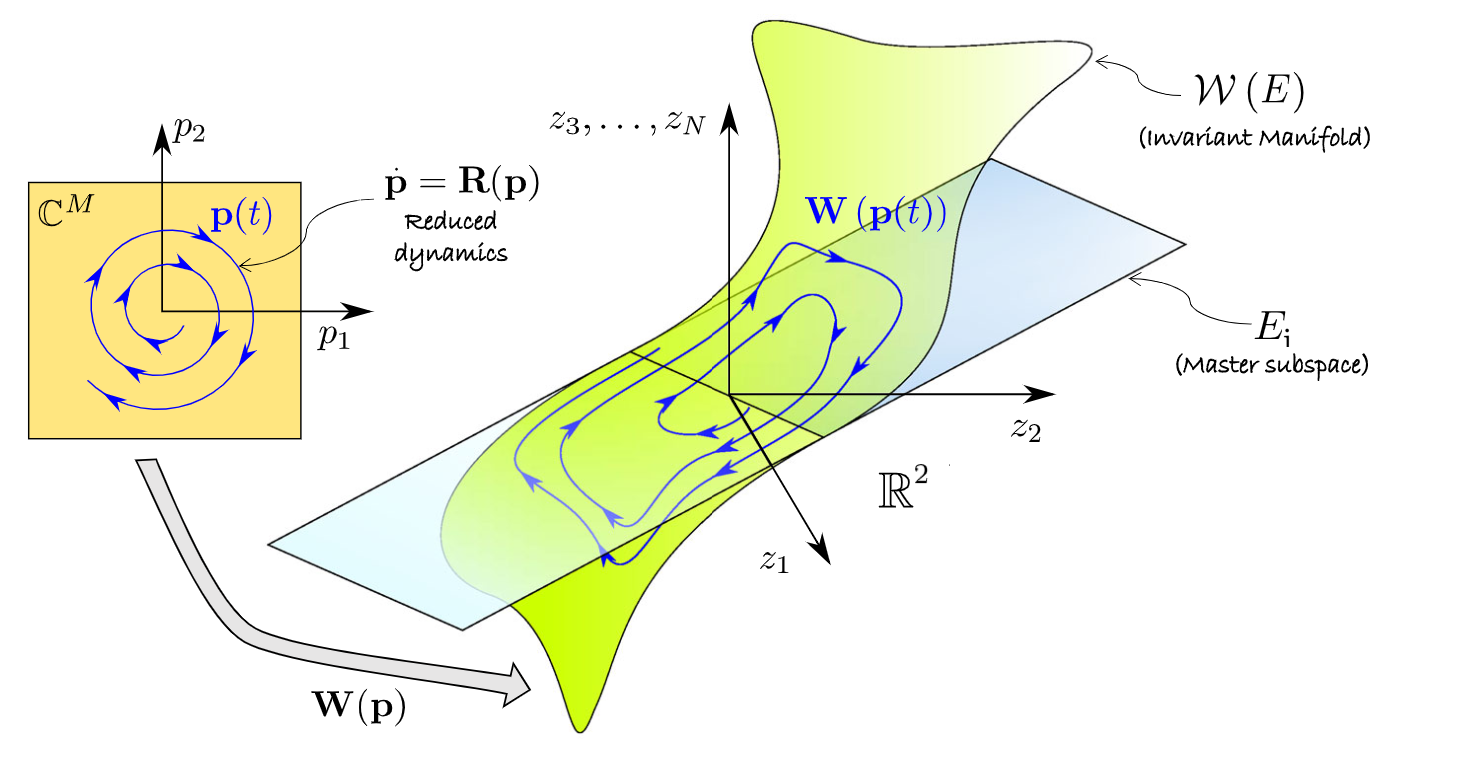
The reduced dynamics for such a system are given as
 .
.
To obtain an analytical expression for a backbone curve the
parametrisation coordinates are transformed to polar notation. We
set
![$$\mathbf{p} = [p, \bar{p}] = [\rho e^{i\theta}, \rho e^{-i\theta}]$](Backbone_Curves_eq06188098032939741758-Rescaled.png) $ . In the new coordinates the reduced dynamics read
$ . In the new coordinates the reduced dynamics read
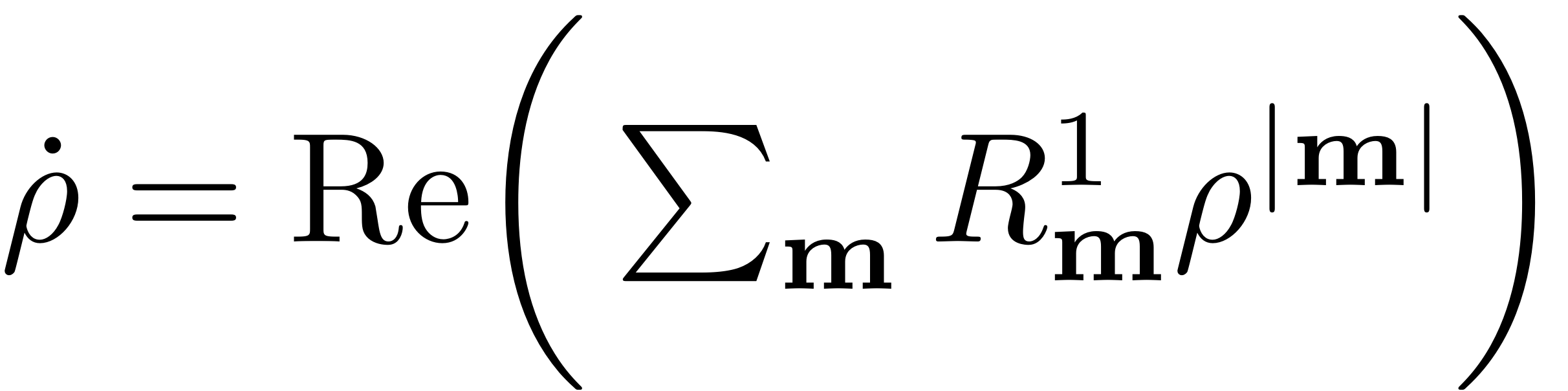
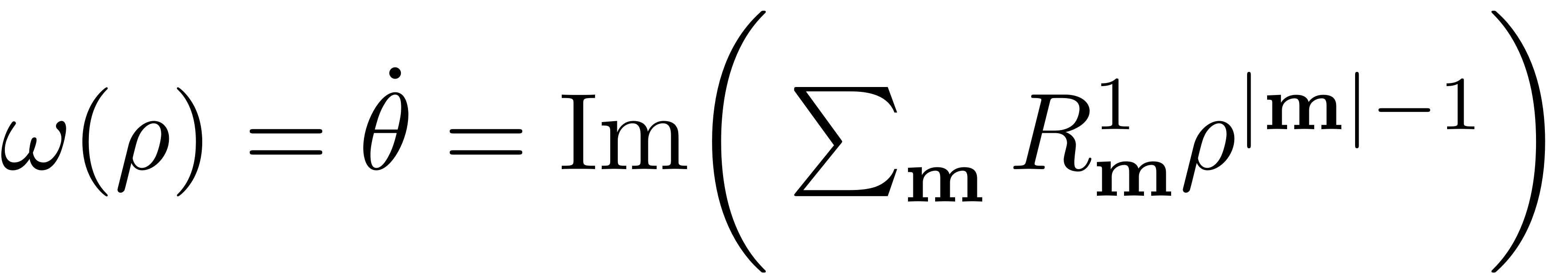
For each polar amplitude a unique change in polar angle
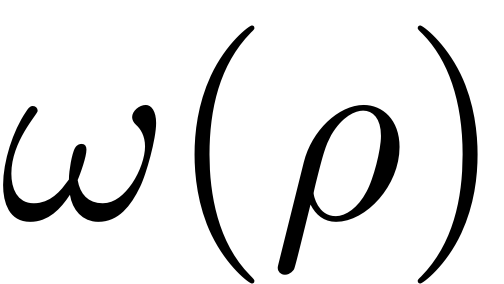 thus results. This prompts us to define the backbone curve in this
context as the collection of points which follow this analytical
relation (cf. Szalai, Erhardt & Haller 20017, Haller, Pedergnana
& Ponsioen 2018).
thus results. This prompts us to define the backbone curve in this
context as the collection of points which follow this analytical
relation (cf. Szalai, Erhardt & Haller 20017, Haller, Pedergnana
& Ponsioen 2018).
Now consider a particular amplitude
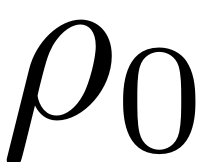 in the polar parametrisation space. The amplitude of a corresponding
nonlinear periodic orbit of the full nonlinear physical system which
oscillates with frequency
in the polar parametrisation space. The amplitude of a corresponding
nonlinear periodic orbit of the full nonlinear physical system which
oscillates with frequency
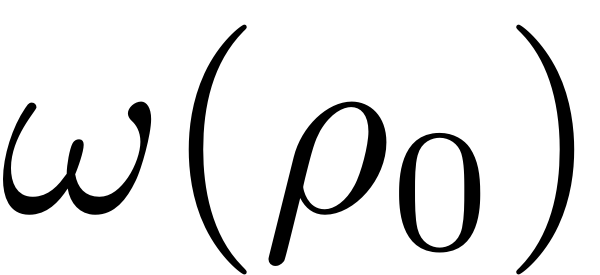 is then given by
is then given by
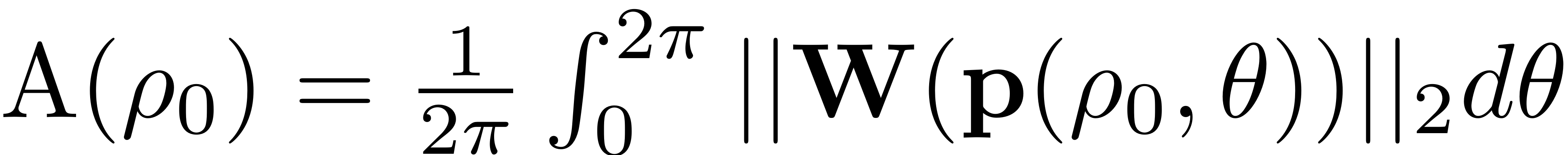 .
.
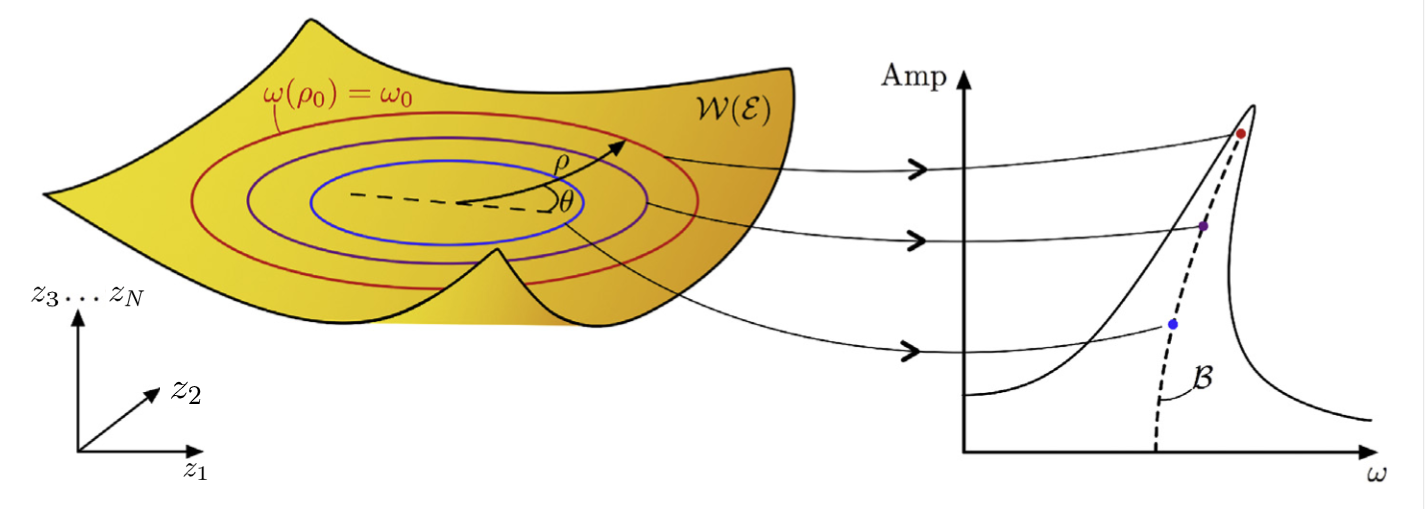
Thus, in the full system, the backbone curve computed on the SSM is
given by the set
 . A depiction of this process is shown in the following figure (cf.
Ponsioen, Pedergnana & Haller 2018)
. A depiction of this process is shown in the following figure (cf.
Ponsioen, Pedergnana & Haller 2018)
Example
As an example, we take the system of an <oscillatory chain.html > with cubic nonlinearities, as treated in our toolbox.
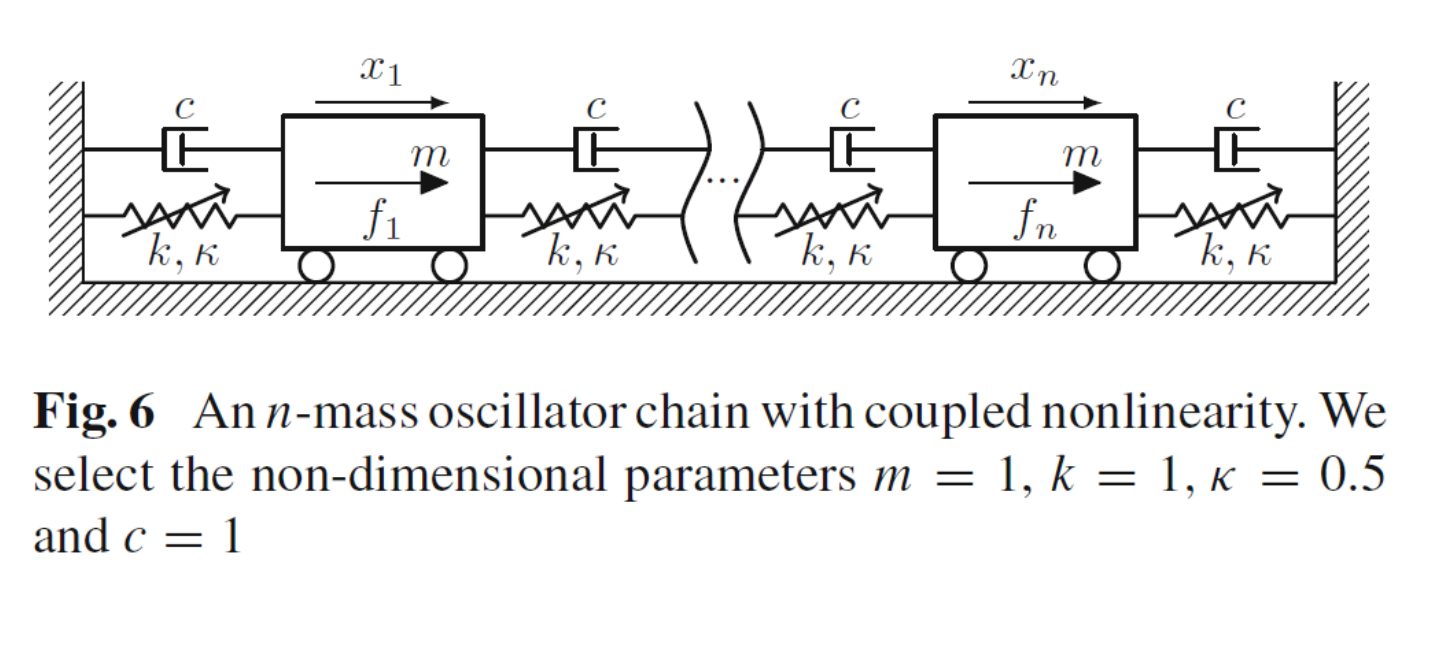
Setup
clear DS S n = 10; m = 1; k = 1; c = 0.1; kappa2 = 0; kappa3 = 0.5; [M,C,K,fnl,~] = build_model(n,m,c,k,kappa2,kappa3); DS = DynamicalSystem(); set(DS,'M',M,'C',C,'K',K,'fnl',fnl); set(DS.Options,'Emax',5,'Nmax',10,'notation','multiindex')
To analyse the nonlinear forced response of the assume periodic forcing of the form
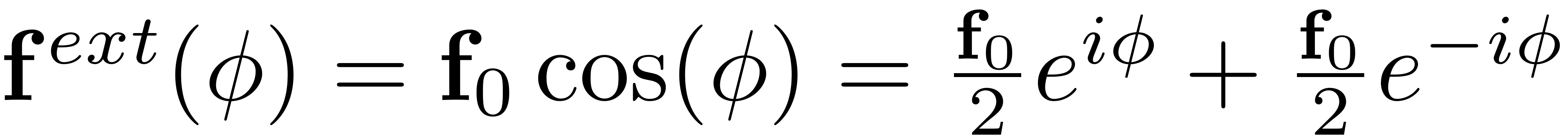
with amplitued
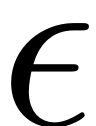 .
.
epsilon = 5e-3; f_0 = ones(n,1); kappas = [-1; 1]; coeffs = [f_0 f_0]/2; DS.add_forcing(coeffs, kappas,epsilon);
Linear Modal analysis and SSM setup
[V,D,W] = DS.linear_spectral_analysis();
Due to high-dimensionality, we compute only the first 5 eigenvalues with the smallest magnitude. These would also be used to compute the spectral quotients Assuming a proportional damping hypthesis with symmetric matrices modal damping ratio for 1 mode is 1.423148e-02 modal damping ratio for 2 mode is 2.817326e-02 modal damping ratio for 3 mode is 4.154150e-02 modal damping ratio for 4 mode is 5.406408e-02 modal damping ratio for 5 mode is 6.548607e-02 The first 10 nonzero eigenvalues are given as -0.0041 + 0.2846i -0.0041 - 0.2846i -0.0159 + 0.5632i -0.0159 - 0.5632i -0.0345 + 0.8301i -0.0345 - 0.8301i -0.0585 + 1.0797i -0.0585 - 1.0797i -0.0858 + 1.3069i -0.0858 - 1.3069i
Choose Master subspace (perform resonance analysis)
S = SSM(DS); set(S.Options, 'reltol', 0.1,'notation','multiindex') masterModes = [1,2]; S.choose_E(masterModes);
(near) outer resonance detected for the following combination of master eigenvalues
2 0
3 1
4 2
5 3
6 4
0 2
1 3
2 4
3 5
4 6
4 1
5 2
6 3
1 4
2 5
3 6
These are in resonance with the follwing eigenvalues of the slave subspace
-0.0159 + 0.5632i
-0.0159 + 0.5632i
-0.0159 + 0.5632i
-0.0159 + 0.5632i
-0.0159 + 0.5632i
-0.0159 - 0.5632i
-0.0159 - 0.5632i
-0.0159 - 0.5632i
-0.0159 - 0.5632i
-0.0159 - 0.5632i
-0.0345 + 0.8301i
-0.0345 + 0.8301i
-0.0345 + 0.8301i
-0.0345 - 0.8301i
-0.0345 - 0.8301i
-0.0345 - 0.8301i
sigma_out = 21
(near) inner resonance detected for the following combination of master eigenvalues
2 1
3 2
4 3
1 2
2 3
3 4
These are in resonance with the follwing eigenvalues of the master subspace
-0.0041 + 0.2846i
-0.0041 + 0.2846i
-0.0041 + 0.2846i
-0.0041 - 0.2846i
-0.0041 - 0.2846i
-0.0041 - 0.2846i
sigma_in = 21
Setup SSM computation
We choose to use a continuation based approach to obtain the FRC directly from the ROM on the SSM. The following parameters are chosen for continuation.
order = 7; % Approximation order outdof = floor(n/2); set(S.Options, 'reltol', 1,'IRtol',0.02,'notation', 'multiindex') set(S.FRCOptions, 'nt', 2^7, 'nPar', 100, 'outdof',outdof) set(S.FRCOptions, 'method','continuation ep') set(S.contOptions,'h0',0.01,'h_max',0.1)
choose frequency range
omega0 = imag(S.E.spectrum(1)); omegaRange = omega0*[0.8 1.2]; % Extract Backbone Curve BB = S.extract_backbone(masterModes,omegaRange, order);
(near) outer resonance detected for the following combination of master eigenvalues
2 0
2 1
3 1
3 2
4 2
4 3
5 3
5 4
6 4
0 2
1 2
1 3
2 3
2 4
3 4
3 5
4 5
4 6
2 0
3 0
3 1
4 1
4 2
5 2
5 3
6 3
6 4
0 2
0 3
1 3
1 4
2 4
2 5
3 5
3 6
4 6
3 0
4 0
4 1
5 1
5 2
6 2
6 3
7 3
0 3
0 4
1 4
1 5
2 5
2 6
3 6
3 7
4 0
5 0
5 1
6 1
6 2
7 2
7 3
0 4
0 5
1 5
1 6
2 6
2 7
3 7
These are in resonance with the follwing eigenvalues of the slave subspace
-0.0159 + 0.5632i
-0.0159 + 0.5632i
-0.0159 + 0.5632i
-0.0159 + 0.5632i
-0.0159 + 0.5632i
-0.0159 + 0.5632i
-0.0159 + 0.5632i
-0.0159 + 0.5632i
-0.0159 + 0.5632i
-0.0159 - 0.5632i
-0.0159 - 0.5632i
-0.0159 - 0.5632i
-0.0159 - 0.5632i
-0.0159 - 0.5632i
-0.0159 - 0.5632i
-0.0159 - 0.5632i
-0.0159 - 0.5632i
-0.0159 - 0.5632i
-0.0345 + 0.8301i
-0.0345 + 0.8301i
-0.0345 + 0.8301i
-0.0345 + 0.8301i
-0.0345 + 0.8301i
-0.0345 + 0.8301i
-0.0345 + 0.8301i
-0.0345 + 0.8301i
-0.0345 + 0.8301i
-0.0345 - 0.8301i
-0.0345 - 0.8301i
-0.0345 - 0.8301i
-0.0345 - 0.8301i
-0.0345 - 0.8301i
-0.0345 - 0.8301i
-0.0345 - 0.8301i
-0.0345 - 0.8301i
-0.0345 - 0.8301i
-0.0585 + 1.0797i
-0.0585 + 1.0797i
-0.0585 + 1.0797i
-0.0585 + 1.0797i
-0.0585 + 1.0797i
-0.0585 + 1.0797i
-0.0585 + 1.0797i
-0.0585 + 1.0797i
-0.0585 - 1.0797i
-0.0585 - 1.0797i
-0.0585 - 1.0797i
-0.0585 - 1.0797i
-0.0585 - 1.0797i
-0.0585 - 1.0797i
-0.0585 - 1.0797i
-0.0585 - 1.0797i
-0.0858 + 1.3069i
-0.0858 + 1.3069i
-0.0858 + 1.3069i
-0.0858 + 1.3069i
-0.0858 + 1.3069i
-0.0858 + 1.3069i
-0.0858 + 1.3069i
-0.0858 - 1.3069i
-0.0858 - 1.3069i
-0.0858 - 1.3069i
-0.0858 - 1.3069i
-0.0858 - 1.3069i
-0.0858 - 1.3069i
-0.0858 - 1.3069i
sigma_out = 21
(near) inner resonance detected for the following combination of master eigenvalues
2 1
3 2
4 3
5 4
1 2
2 3
3 4
4 5
These are in resonance with the follwing eigenvalues of the master subspace
-0.0041 + 0.2846i
-0.0041 + 0.2846i
-0.0041 + 0.2846i
-0.0041 + 0.2846i
-0.0041 - 0.2846i
-0.0041 - 0.2846i
-0.0041 - 0.2846i
-0.0041 - 0.2846i
sigma_in = 21
Due to (near) outer resonance, the exisitence of the manifold is questionable and the underlying computation may suffer.
Attempting manifold computation
Manifold computation time at order 2 = 00:00:00
Estimated memory usage at order 2 = 1.70E-02 MB
Manifold computation time at order 3 = 00:00:00
Estimated memory usage at order 3 = 2.24E-02 MB
Manifold computation time at order 4 = 00:00:00
Estimated memory usage at order 4 = 3.25E-02 MB
Manifold computation time at order 5 = 00:00:00
Estimated memory usage at order 5 = 4.51E-02 MB
Manifold computation time at order 6 = 00:00:00
Estimated memory usage at order 6 = 6.22E-02 MB
Manifold computation time at order 7 = 00:00:00
Estimated memory usage at order 7 = 8.40E-02 MB
gamma =
0.0000 + 0.0024i
-0.0000 - 0.0000i
-0.0000 + 0.0000i
Total time spent on backbone curve computation = 00:00:01
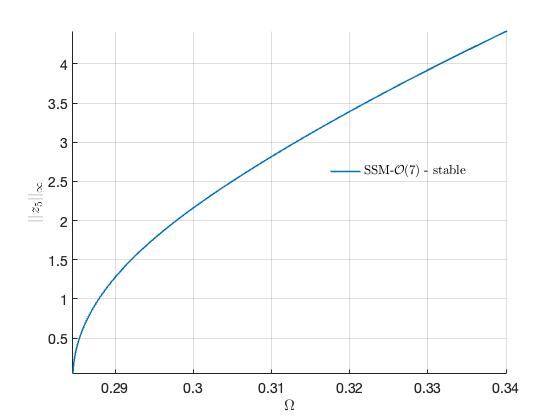
Extract Forced Response Curve
FRC = S.extract_FRC('freq',omegaRange,order);
*****************************************
Calculating FRC using SSM with master subspace: [1 2]
(near) outer resonance detected for the following combination of master eigenvalues
2 0
2 1
3 1
3 2
4 2
4 3
5 3
5 4
6 4
0 2
1 2
1 3
2 3
2 4
3 4
3 5
4 5
4 6
2 0
3 0
3 1
4 1
4 2
5 2
5 3
6 3
6 4
0 2
0 3
1 3
1 4
2 4
2 5
3 5
3 6
4 6
3 0
4 0
4 1
5 1
5 2
6 2
6 3
7 3
0 3
0 4
1 4
1 5
2 5
2 6
3 6
3 7
4 0
5 0
5 1
6 1
6 2
7 2
7 3
0 4
0 5
1 5
1 6
2 6
2 7
3 7
These are in resonance with the follwing eigenvalues of the slave subspace
-0.0159 + 0.5632i
-0.0159 + 0.5632i
-0.0159 + 0.5632i
-0.0159 + 0.5632i
-0.0159 + 0.5632i
-0.0159 + 0.5632i
-0.0159 + 0.5632i
-0.0159 + 0.5632i
-0.0159 + 0.5632i
-0.0159 - 0.5632i
-0.0159 - 0.5632i
-0.0159 - 0.5632i
-0.0159 - 0.5632i
-0.0159 - 0.5632i
-0.0159 - 0.5632i
-0.0159 - 0.5632i
-0.0159 - 0.5632i
-0.0159 - 0.5632i
-0.0345 + 0.8301i
-0.0345 + 0.8301i
-0.0345 + 0.8301i
-0.0345 + 0.8301i
-0.0345 + 0.8301i
-0.0345 + 0.8301i
-0.0345 + 0.8301i
-0.0345 + 0.8301i
-0.0345 + 0.8301i
-0.0345 - 0.8301i
-0.0345 - 0.8301i
-0.0345 - 0.8301i
-0.0345 - 0.8301i
-0.0345 - 0.8301i
-0.0345 - 0.8301i
-0.0345 - 0.8301i
-0.0345 - 0.8301i
-0.0345 - 0.8301i
-0.0585 + 1.0797i
-0.0585 + 1.0797i
-0.0585 + 1.0797i
-0.0585 + 1.0797i
-0.0585 + 1.0797i
-0.0585 + 1.0797i
-0.0585 + 1.0797i
-0.0585 + 1.0797i
-0.0585 - 1.0797i
-0.0585 - 1.0797i
-0.0585 - 1.0797i
-0.0585 - 1.0797i
-0.0585 - 1.0797i
-0.0585 - 1.0797i
-0.0585 - 1.0797i
-0.0585 - 1.0797i
-0.0858 + 1.3069i
-0.0858 + 1.3069i
-0.0858 + 1.3069i
-0.0858 + 1.3069i
-0.0858 + 1.3069i
-0.0858 + 1.3069i
-0.0858 + 1.3069i
-0.0858 - 1.3069i
-0.0858 - 1.3069i
-0.0858 - 1.3069i
-0.0858 - 1.3069i
-0.0858 - 1.3069i
-0.0858 - 1.3069i
-0.0858 - 1.3069i
sigma_out = 21
(near) inner resonance detected for the following combination of master eigenvalues
2 1
3 2
4 3
5 4
1 2
2 3
3 4
4 5
These are in resonance with the follwing eigenvalues of the master subspace
-0.0041 + 0.2846i
-0.0041 + 0.2846i
-0.0041 + 0.2846i
-0.0041 + 0.2846i
-0.0041 - 0.2846i
-0.0041 - 0.2846i
-0.0041 - 0.2846i
-0.0041 - 0.2846i
sigma_in = 21
Due to (near) outer resonance, the exisitence of the manifold is questionable and the underlying computation may suffer.
Attempting manifold computation
Manifold computation time at order 2 = 00:00:00
Estimated memory usage at order 2 = 1.70E-02 MB
Manifold computation time at order 3 = 00:00:00
Estimated memory usage at order 3 = 2.24E-02 MB
Manifold computation time at order 4 = 00:00:00
Estimated memory usage at order 4 = 3.25E-02 MB
Manifold computation time at order 5 = 00:00:00
Estimated memory usage at order 5 = 4.51E-02 MB
Manifold computation time at order 6 = 00:00:00
Estimated memory usage at order 6 = 6.22E-02 MB
Manifold computation time at order 7 = 00:00:00
Estimated memory usage at order 7 = 8.40E-02 MB
Run='freqSubint1.ep': Continue equilibria along primary branch.
STEP DAMPING NORMS COMPUTATION TIMES
IT SIT GAMMA ||d|| ||f|| ||U|| F(x) DF(x) SOLVE
0 7.62e-06 8.44e+00 0.0 0.0 0.0
1 1 1.00e+00 4.49e-05 4.53e-12 8.44e+00 0.0 0.0 0.0
2 1 1.00e+00 3.49e-10 1.56e-16 8.44e+00 0.0 0.0 0.0
STEP TIME ||U|| LABEL TYPE om rho1 th1 eps
0 00:00:00 8.4360e+00 1 EP 2.8461e-01 1.6869e+00 5.7146e+00 5.0000e-03
10 00:00:00 8.5208e+00 2 2.7791e-01 1.2016e+00 5.8975e+00 5.0000e-03
20 00:00:00 8.6918e+00 3 2.6101e-01 5.2987e-01 6.1176e+00 5.0000e-03
25 00:00:00 8.7973e+00 4 EP 2.2768e-01 2.2778e-01 6.2123e+00 5.0000e-03
STEP TIME ||U|| LABEL TYPE om rho1 th1 eps
0 00:00:00 8.4360e+00 5 EP 2.8461e-01 1.6869e+00 5.7146e+00 5.0000e-03
10 00:00:00 8.3414e+00 6 2.9084e-01 2.1513e+00 5.4842e+00 5.0000e-03
20 00:00:01 8.0042e+00 7 2.9893e-01 2.6475e+00 4.9935e+00 5.0000e-03
30 00:00:01 7.3774e+00 8 3.0167e-01 2.6662e+00 4.4736e+00 5.0000e-03
31 00:00:01 7.3641e+00 9 SN 3.0167e-01 2.6626e+00 4.4648e+00 5.0000e-03
31 00:00:01 7.3641e+00 10 FP 3.0167e-01 2.6626e+00 4.4648e+00 5.0000e-03
40 00:00:01 6.4602e+00 11 2.9961e-01 2.2176e+00 3.9824e+00 5.0000e-03
50 00:00:01 5.6676e+00 12 2.9747e-01 1.5851e+00 3.6687e+00 5.0000e-03
52 00:00:01 5.5699e+00 13 SN 2.9742e-01 1.4924e+00 3.6327e+00 5.0000e-03
52 00:00:01 5.5699e+00 14 FP 2.9742e-01 1.4924e+00 3.6327e+00 5.0000e-03
60 00:00:01 5.0425e+00 15 3.0015e-01 9.1890e-01 3.4321e+00 5.0000e-03
70 00:00:01 4.5896e+00 16 3.3742e-01 2.4657e-01 3.2183e+00 5.0000e-03
71 00:00:01 4.5806e+00 17 EP 3.4152e-01 2.2876e-01 3.2128e+00 5.0000e-03
Total time spent on FRC computation upto O(7) = 00:00:03
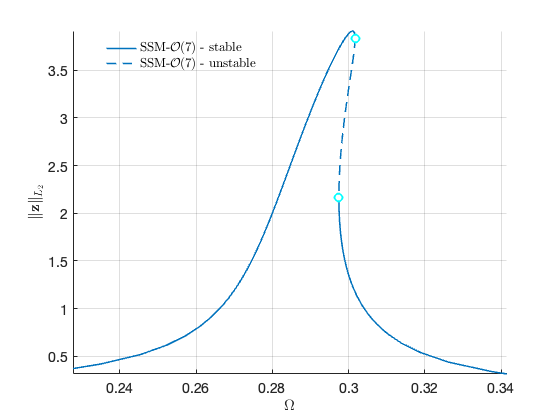
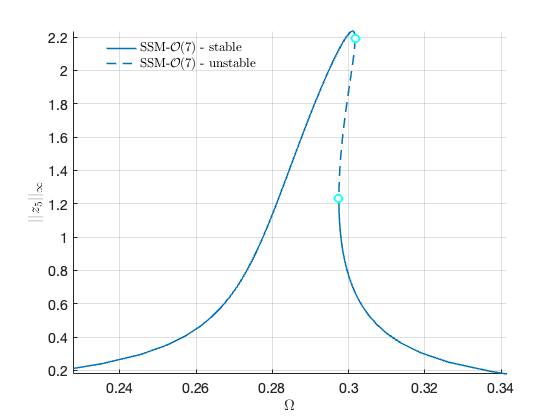
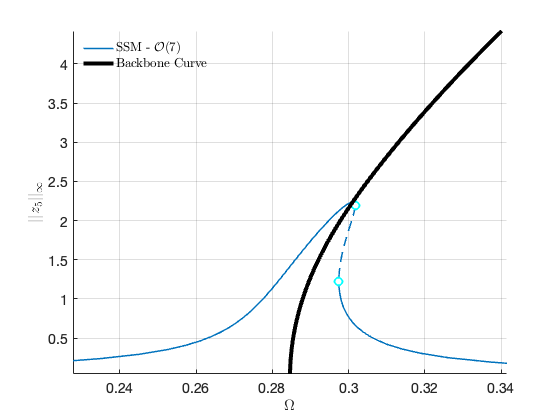
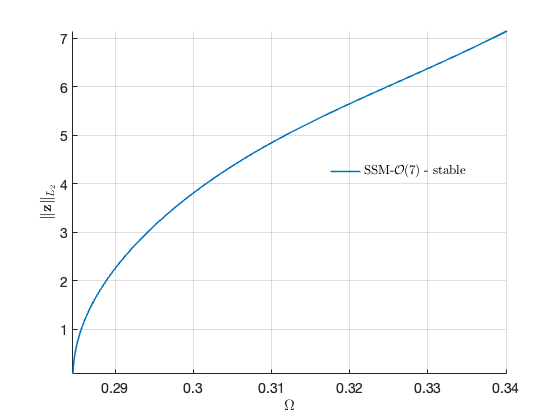
Now we proceed to plot the backbone curve on top of the forced response, for visualising the relation between the two quantities.
hold on; plot([BB.Omega],[BB.Aout], 'Color' , 'black', 'LineWidth',4) legend('$$\textrm{SSM - }\mathcal{O}(7)$$','','Backbone Curve','Interpreter','latex')