COHOMOLOGICAL_SOLUTION
Contents
function [W_0i, R_0i,multi_input] = cohomological_solution(obj, i, W_0, R_0,multi_input,DStype)
This function computes the solution of the invariance equation at order i. The function computes the SSM where we solve the invariance equation

of the dynamical system
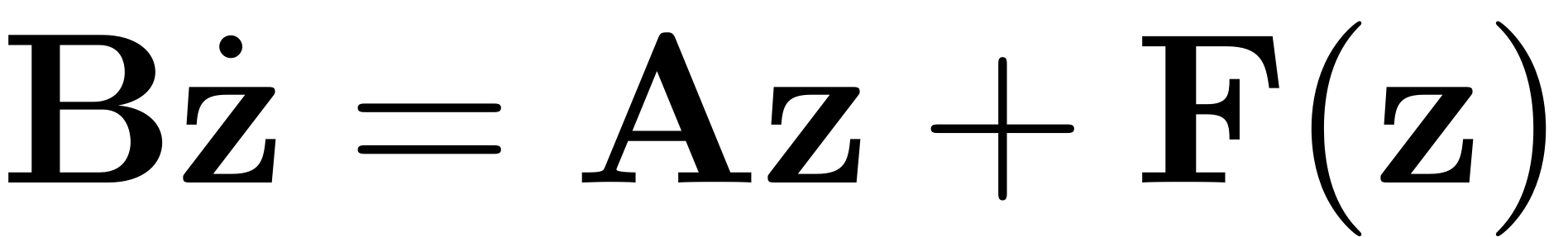 .
.
Tensor based computation
The SSM is expressed in terms of the expansion
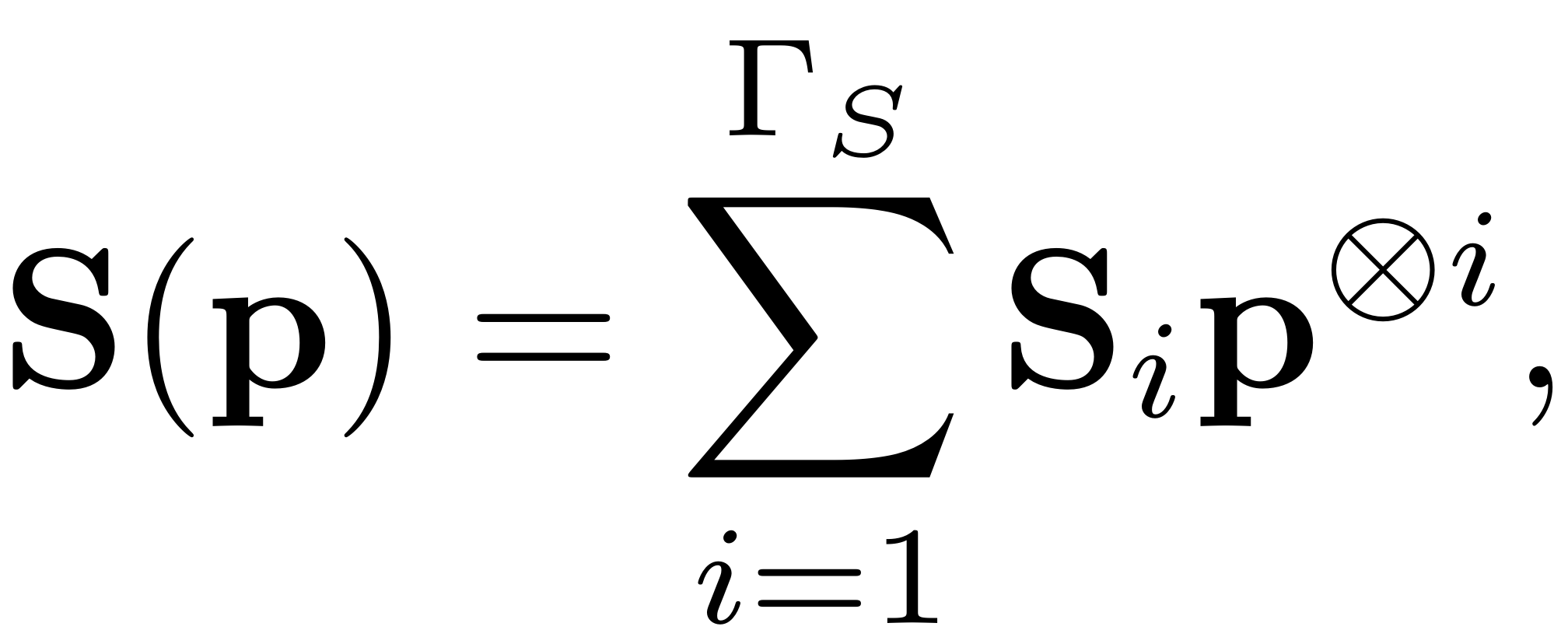
where
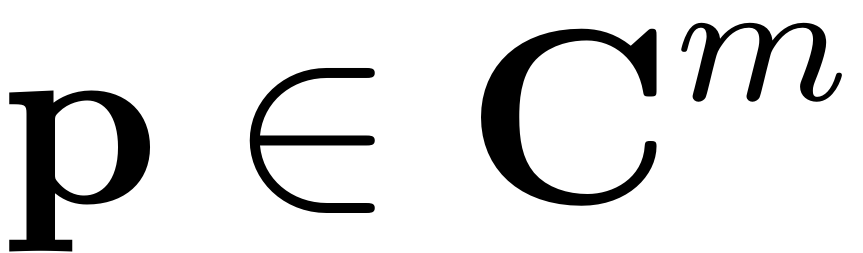 are parameterization coordinates of the
are parameterization coordinates of the
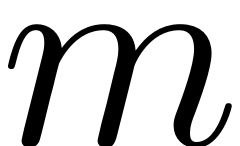 -dimensional SSM.
-dimensional SSM.
The coefficients at different orders are collected in a cell array
 , where
, where
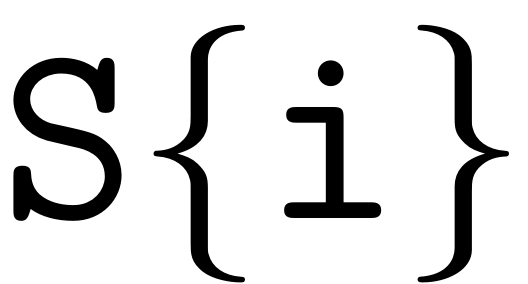 gives the coefficients at order
gives the coefficients at order
 , i.e.
, i.e.
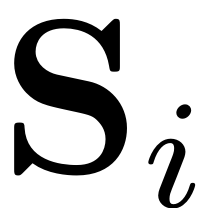 . These are obtained by solving for
. These are obtained by solving for
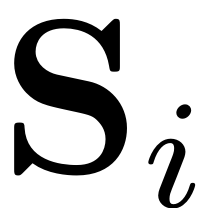 in the following equation
in the following equation
where
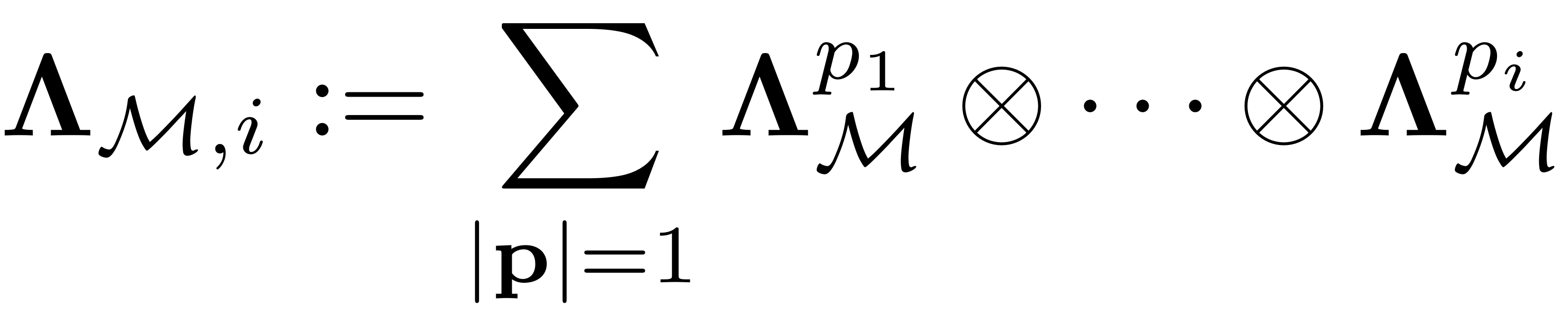
and
 is a diagonal (
is a diagonal ( ) matrix containing the eigenvalues of the master modal subspace
) matrix containing the eigenvalues of the master modal subspace
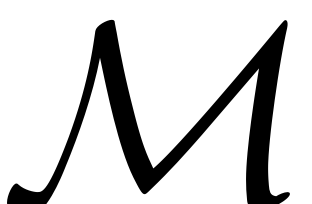 . The above equation in the vectorized notation is given by
. The above equation in the vectorized notation is given by
![$$\underbrace{\left[\left(\mathbf{\Lambda}_{\mathcal{M},i}^{\top}\otimes\mathbf{B}\right)-\left(\mathbf{I}_{m^{i}}\otimes\mathbf{A}\right)\right]}_{{\mathcal{C}}_{i}}\textrm{vec}\left(\mathbf{S}_{i}\right)=\textrm{vec}\left(\mathbf{L}_{i}\right)-\left(\mathbf{I}_{m^{i}}\otimes\mathbf{B}\mathbf{S}_{1}\right)\textrm{vec}\left(\mathbf{R}_{i}\right)$$](cohomological_solution_eq03579440951638808804-Rescaled.png)
Here
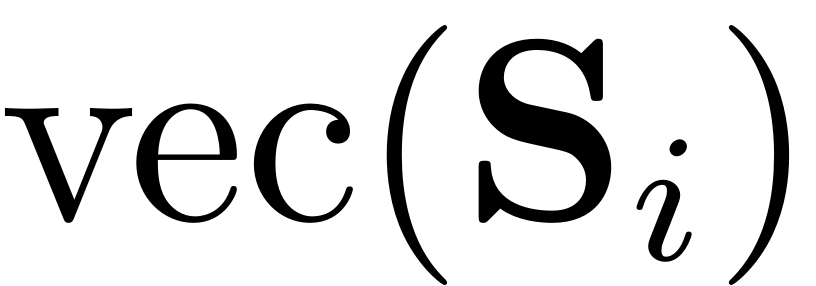 just stands for the vectorization operator in MATLAB obtained by the
command
just stands for the vectorization operator in MATLAB obtained by the
command
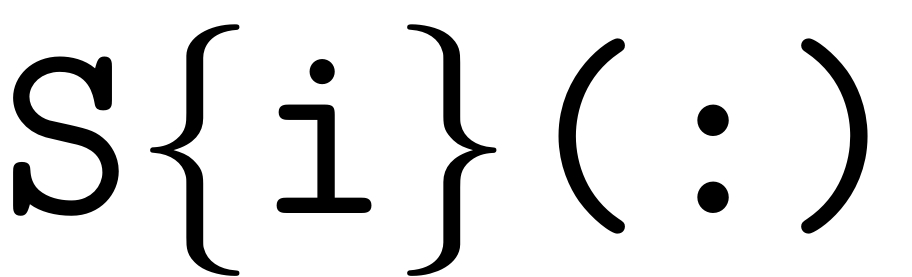 .
.
switch obj.Options.notation case 'tensor'
Lambda_M = obj.E.spectrum;
A = obj.System.A; % A matrix
B = obj.System.B; % B matrix
W_M = obj.E.adjointBasis; % Right eigenvectors of the modal subspace
V_M = obj.E.basis; % Left eigenvectors of the modal subspace
N = obj.dimSystem; % Full system dimensionality in first-order form
F = obj.System.F; % Full system Nonlinearity coefficients at different orders
m = length(Lambda_M); % dim(M): M is the master modal subspace
N_i = N*m^i; % number of unknown SSM coefficients in the tensor notation at order i
ref = min(abs(Lambda_M));
if ref<1e-10; ref = max(abs(Lambda_M)); end
abstol = obj.Options.reltol * ref;
Assemble the coefficient matrix of SSM
Obtaining
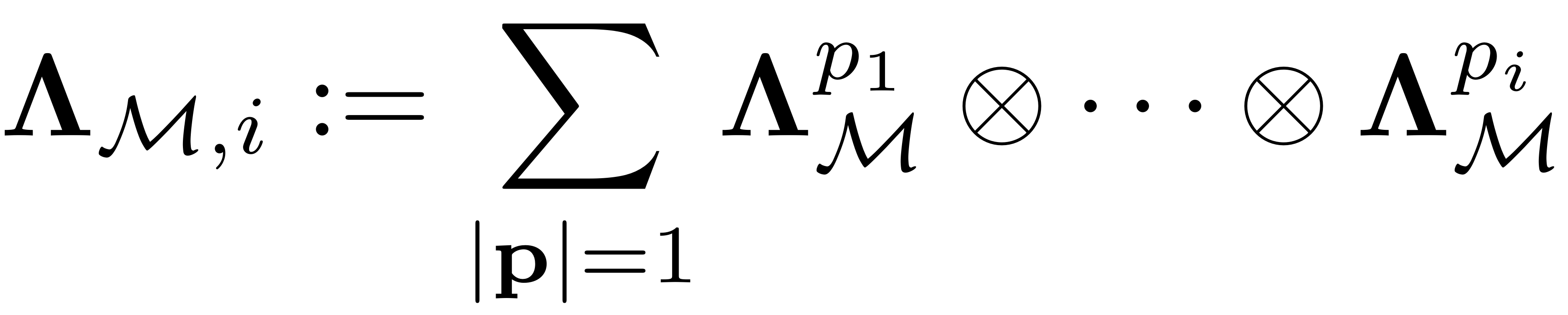
We assemble it as
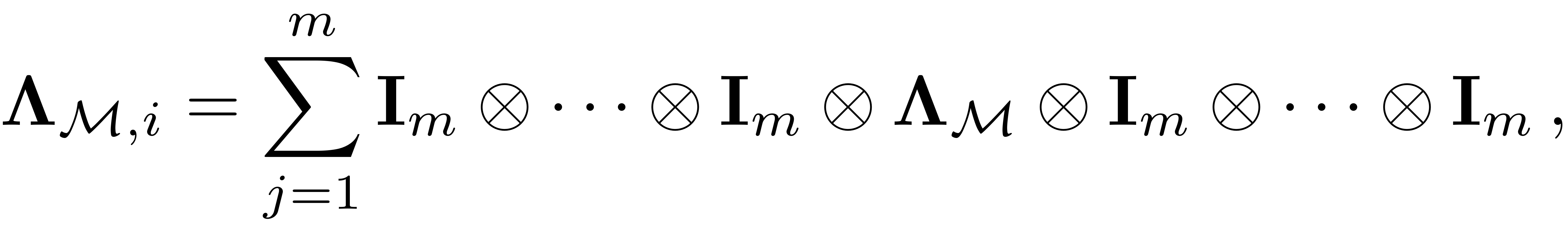
where each term is a kronecker product of
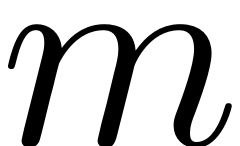 matrices and
matrices and
 occurs at the
occurs at the
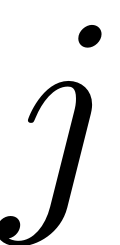 -th location.
-th location.
We can show that the diagonal matrix
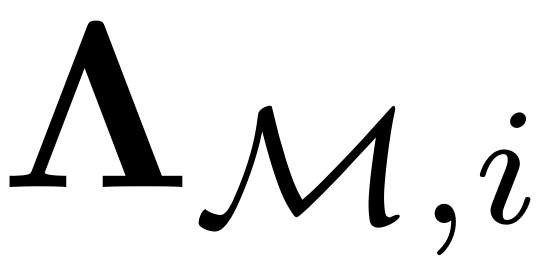 contains
contains
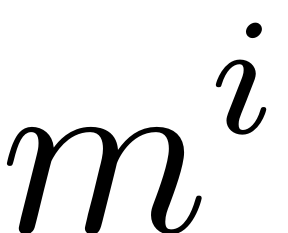 non-zero elements
non-zero elements
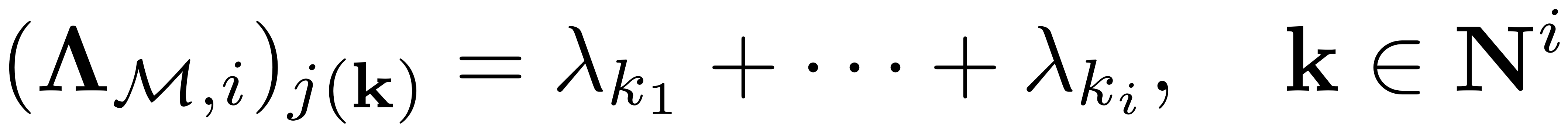 and
and
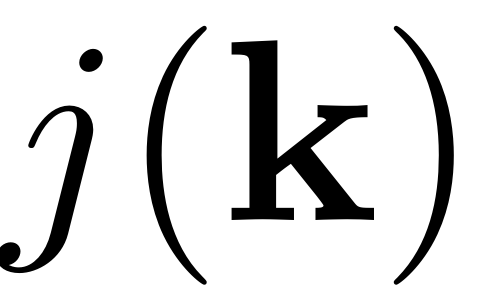 represents the lexicographical bijective indexing of
represents the lexicographical bijective indexing of
 -tuples taking values from
-tuples taking values from
 and is given by the
and is given by the combinator function.
disp(['Computing autonomous whisker at order ' num2str(i)]) combinations = combinator(m,i,'p','r'); Lambda_Mi = sum(Lambda_M(combinations),2);
Spectrum of
![$\mathcal{C}_i:=\left[\left(\mathbf{\Lambda}_{\mathcal{M},i}^{\top}\otimes\mathbf{B}\right)-\left(\mathbf{I}_{m^{i}}\otimes\mathbf{A}\right)\right]$](cohomological_solution_eq10981965585988729351-Rescaled.png)
The matrix that needs to be inverted for solving the coefficients at
the
 -th order is given by
-th order is given by
![$$\mathcal{C}_i:=\left[\left(\mathbf{\Lambda}_{\mathcal{M},i}^{\top}\otimes\mathbf{B}\right)-\left(\mathbf{I}_{m^{i}}\otimes\mathbf{A}\right)\right]$$](cohomological_solution_eq17123965705113596086-Rescaled.png)
Assemble RHS
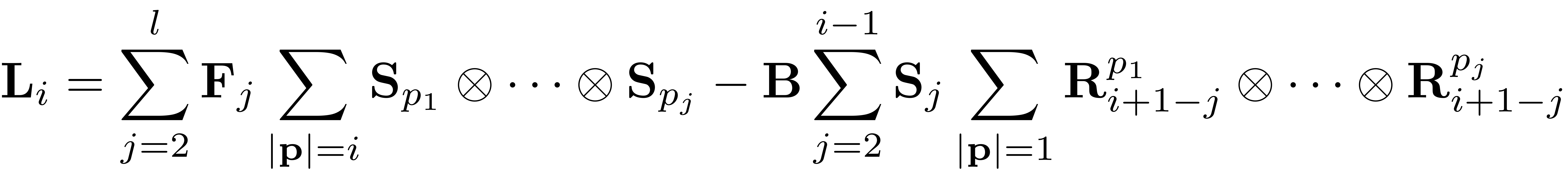
where
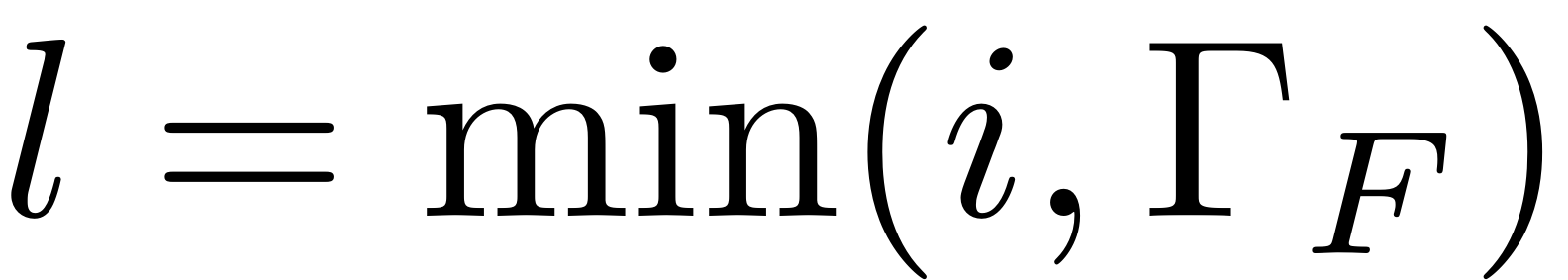 since we need to compute the summation at most up to the order of
the nonlinearity in
since we need to compute the summation at most up to the order of
the nonlinearity in
 .
.
SIZE = [N, m*ones(1,i)];
FS = sptensor(SIZE);
First term
l = min(i,length(F));
for j = 2:l % Outer for loop can be parallelized - l cores
% find values for j positive numbers summing up to i
P = nsumk(j,i,'positive');
FS = FS + tensor_composition(F{j},W_0,P,SIZE);
end
Second term
SR = sptensor(SIZE);
% R_0i = R_0(i:-1:2); % used for parfor
for j = 2:i-1 % Outer for loop can be parallelized - i-1 cores
P = ones(j,j) + eye(j,j);
R_j = {sptensor(speye(m,m)),R_0{i+1-j}};
% R_j = {sptensor(speye(m,m)),R_0i{j}}; % used for parfor
SR = SR + tensor_composition(W_0{j},R_j,P,SIZE);
end
if m==1 % tensor_toolbox has issues
if ~isempty(FS.vals)
FS = sparse(FS.subs(:,1), FS.subs(:,2), FS.vals, N_i, 1);
else
FS = sparse(N_i,1);
end
if ~isempty(SR.vals)
SR = sparse(SR.subs(:,1), SR.subs(:,2), SR.vals, N_i, 1);
else
SR = sparse(N_i,1);
end
L_i = FS - B*SR;
else
L_i = FS - ttm(SR,B,1);
Convert
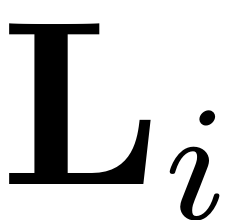 object to sparse vector.
object to sparse vector.
L_i = sptenmat(permute(L_i,[1, ndims(L_i):-1:2]), 1:ndims(L_i));
if isempty(L_i.vals)
L_i = sparse(N_i,1);
else
L_i = sparse(L_i.subs(:,1),L_i.subs(:,2),L_i.vals,N_i,1);
end
L_i = reshape(L_i,N,[]);
end
Solving for SSM coefficients and Reduced dynamics
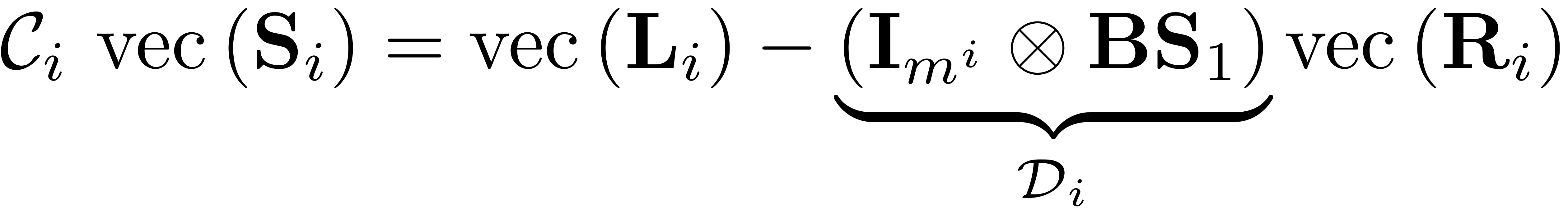
W_0i = zeros(N,m^i); % generally dense R_0i = sparse(m,m^i); nRes = 0; paramStyle = obj.Options.paramStyle; parfor l = 1:m^i
lambda_l = Lambda_Mi(l);
C_l = lambda_l * B - A;
L_il = L_i(:,l);
Checking for near-inner resonances.
J = find(abs(lambda_l - Lambda_M)<abstol);
if ~isempty(J)
switch paramStyle
case 'normalform'
Choosing reduced dynamics using (near-)kernel of
 .
.
R_0il = zeros(m,1); % for slicing use for j = J w_j = W_M(:,j); % R_0i(j,l) = w_j'*L_il; R_0il(j) = w_j'*L_il; end R_0i(:,l) = R_0il;
case 'graph' R_0i(:,l) = W_M'*L_il; end b_l = L_il - B * V_M * R_0i(:,l); else b_l = L_il; end nRes = nRes + numel(J);
Obtaining minimum-norm solution for
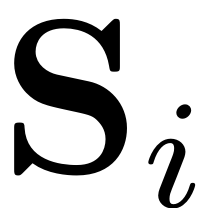 using
using
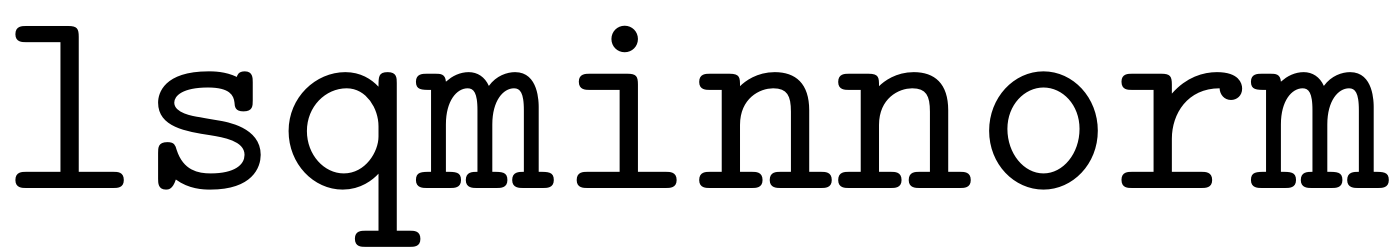 which performs a complete orthogonal decomposition and is better
suited for sparse matrices as opposed to the Moore-Penrose
pseudo-inverse (
which performs a complete orthogonal decomposition and is better
suited for sparse matrices as opposed to the Moore-Penrose
pseudo-inverse (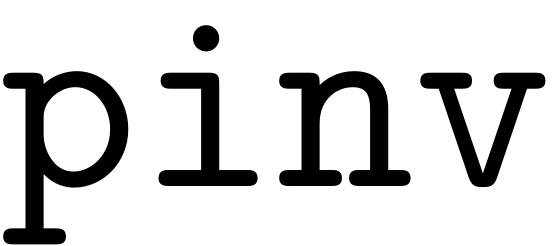 ). We would like to use better iterative procedures moving forward,
currently lsqlin is not suited for complex data entries.
). We would like to use better iterative procedures moving forward,
currently lsqlin is not suited for complex data entries.
W_0i(:,l) = solveinveq(C_l,b_l,obj.Options.solver);
end disp([num2str(nRes) ' (near) inner resonance(s) detected at order ' num2str(i)]) W_0i = reshape(sptensor(W_0i(:)), [N, m*ones(1,i)]); R_0i = reshape(sptensor(R_0i(:)), [m, m*ones(1,i)]); W_0i = permute(W_0i,[1, ndims(W_0i):-1:2]); R_0i = permute(R_0i,[1, ndims(R_0i):-1:2]);
case 'multiindex'
k = i; % order of computation N = obj.dimSystem; % Phase space dimension l = numel(obj.E.spectrum); % Manifold dimension % ################################################################ % Setup data structs for passing arguments into functions % system parameters independent of multi- index ordering sys.l = l; sys.N = N; sys.V_M = obj.E.basis; sys.W_M = obj.E.adjointBasis; sys.solver = obj.Options.solver; sys.reltol = obj.Options.reltol; sys.DStype = obj.System.Options.DStype; % data containing information about nonlinearity [NL,nl_data] = NLdata(obj); sys.nl_order = nl_data.order; sys.nl_input_dim = nl_data.nl_input_dim; % ################################################################ % ---- variables that depend on multi-index ordering ---- K = flip(sortrows(nsumk(l,k,'nonnegative')).',2); z_k = data.Z_cci(k); % number of multi_indices if strcmp(sys.DStype,'real') K = K(:,data.revlex2conj{k}(1:z_k)); % conjugate ordered set sys.revlex2conj = data.revlex2conj; % ordering of conjugate set sys.Z_cci = data.Z_cci; % conj. center index end sys.Lambda_M_vector = data.Lambda_M_vector; sys.ordering = data.ordering; sys.z_k = z_k; sys.K = K; sys.k = k; % ################################################################ % ################################################################ % Assemble the right hand side of the invarinace eq. % Mixed Terms WR = zeros(N,z_k); mix = tic; for m = 2:k-1 WR = WR - coeffs_mixed_terms(k,m,W_0,R_0,sys,'aut'); end mixtime = toc(mix); % The composition coefficients of power series if nl_data.intrusion H = data.H; % composition coefficients H_k = coeffs_composition(W_0,H,sys); H{k} = H_k; end % Nonlinearity contributions to invariance equation Fn = zeros(N,z_k); nl = tic; switch nl_data.mode case 'IntrusiveF' sys.symmetry = obj.System.F_semi_sym; % whether function handles are symmetric for n = 2:min(k,nl_data.order) if ~isempty(NL{n}) Fn = Fn + fnl_semiIntrusive(NL{n},W_0,n,K,sys); end end case 'SemiIntrusiveF' sys.symmetry = obj.System.F_semi_sym; % whether function handles are symmetric for n = 2:min(k,nl_data.order) if ~isempty(NL{n}) Fn = Fn + fnl_semiIntrusive(NL{n},W_0,n,K,sys); end end case 'NonIntrusiveF' for n = 2:3 if ~isempty(NL) Fn = Fn + fnl_nonIntrusive(NL,W_0,n,K,sys); end end end nltime = toc(nl); % saving memory if ~any(Fn) Fn = sparse(N,z_k); end if ~any(WR) WR = sparse(N,z_k); end % ################################################################ % ################################################################ % Solving invariance equation and determine reduced dynamics % ################################################################ % Computation for first order dynamical systems if strcmp(obj.Options.COMPtype,'first') A = obj.System.A; % A matrix B = obj.System.B; % B matrix RHS = B*WR + Fn; RHS = reshape(RHS,N*z_k,1); invtic = tic; [R_0i,W_0i,eqtime,rdtime] = Aut_1stOrder_SSM(RHS, sys,A,B); invtime = toc(invtic); % ################################################################# % Computation for second order dynamica lsystems else Mass = obj.System.M; Damp = obj.System.C; Stiff = obj.System.K; invtic = tic; [R_0i,W_0i,eqtime,rdtime] = Aut_2ndOrder_SSM(WR,Fn,sys,Mass,Damp,Stiff); invtime = toc(invtic); end
pass on composition coefficients
if nl_data.intrusion H_k(:,:,1) = W_0i; H{k} = H_k; data.H = H; end obj.solInfo.mixTime(i)= mixtime; obj.solInfo.invTime(i) = invtime; obj.solInfo.eqTime(i) = eqtime; obj.solInfo.nlTime(i) = nltime; obj.solInfo.rdTime(i) = rdtime;
end % estime memory consumption from all variables in the current workspace obj.solInfo.memoryEstimate(i) = monitor_memory('caller');
end function [NL,data] = NLdata(obj)
% NL - contains nonlinearity ot potential % data - contains information about NL data.intrusion = false; data.nl_input_dim = []; intr_opt = obj.System.Options.Intrusion;
Assert that valid option has been chosen for computation
assert(strcmp(intr_opt ,'semi') || strcmp(intr_opt,'none')|| strcmp(intr_opt,'full'),... 'Intrusion options are: full, none, semi') switch obj.System.Options.Intrusion case 'semi' data.mode = 'SemiIntrusiveF'; % Full system nonlinearity handles at different orders NL = obj.System.F_semi; % check input dimensionality of function handles data.nl_input_dim = obj.System.nl_input_dim; case 'none' data.mode = 'NonIntrusiveF'; % Full system nonlinearity handles at different orders NL = obj.System.F_non; % check input dimensionality of function handles data.nl_input_dim = obj.System.nl_input_dim; case 'full' data.intrusion = true; data.mode = 'IntrusiveF'; % Full system nonlinearity coefficients at different orders switch obj.System.order case 1 for j = 2:numel(obj.System.F) if ~isempty(obj.System.F{j}) && nnz(obj.System.F{j})>0 F{j} = @(input) double(ttv( obj.System.F{j},input,2:j+1)); end end case 2 for j = 1:numel(obj.System.fnl) if ~isempty(obj.System.fnl{j}) && nnz(obj.System.fnl{j})>0 F{j+1} = @(input) [-double(ttv( obj.System.fnl{j},input,2:j+2)) ; sparse(obj.System.n,1)]; end end end data.nl_input_dim = obj.System.nl_input_dim; NL = F; end data.order = numel(NL);
end
