fnl_intrusive
Contents
function [pis] = fnl_intrusive(n_mat,k_mat, data)
FNL_INTRUSIVE
This function computes the nonlinear contributions to the invariance
equation for multi indices in set K, given a intrusive tensor fnl.
Computes pi_n_k for every combination of multi-indices in the two
input matrices Multi index arrays n_mat and k_mat need to contain
multi indices of same order n and
k resepectively. The pi's are the forcing contribution
coefficients as given in Computing SSMs using multi indices -
autonomous which can be found in the Documentation.
[pis] = FNL_INTRUSIVE(n_mat,k_mat, field)
- n_mat: multi indices of function which is being composed with parametrisation
- k_mat: multi-indices which characterise the parametrisation
- data: data struct containing necessary information for computation
- pis: composed forcing contributions for the combination of input multi-indices
See also: COHOMOLOGICAL_SOLUTION, DFNL_INTRUSIVE, MULTI_NSUMK
n_pos_idx = any(n_mat); k_pos_idx = any(k_mat); % No calculations for zero multi-indices needed n_zero_idx = find(~n_pos_idx); k_zero_idx = find(~k_pos_idx); switch data.ordering case 'revlex' pis_pos = pi_nk(n_mat(:,n_pos_idx),k_mat(:,k_pos_idx), data); case 'conjugate' %Needs all multi-indices in n_mat and k_mat to have same order pis_pos = pi_nk_conj(n_mat(:,n_pos_idx),k_mat(:,k_pos_idx),data); end
Read results into output array
%insert zero columns if ~isempty(k_zero_idx) pis_cols = zeros(size(pis_pos,1),size(k_mat,2)); pis_cols(:,k_pos_idx) = pis_pos; else pis_cols = pis_pos; end %insert zero rows if ~isempty(n_zero_idx) pis = zeros(size(n_mat,2),size(k_mat,2)); pis(n_pos_idx,:) = pis_cols; else pis = pis_cols; end
Special case
fill pis with ones where k and n_mat both have a zero multiindex
for n_i = n_zero_idx for k_i = k_zero_idx pis(n_i,k_i) = 1; end end
end function [pis] = pi_nk(n_mat,K,data)
assert(nnz(n_mat<0)==0,'Negative multiindices') % Conjugate center index at all orders, for % imaginary system this is empty since then no symmetry is % inherent and we only need the number of multi-indices that % exist at order k, given by nchoosek(k+l-1,l-1) l = size(K,1); % SSM dimension z_k = size(K,2); % Phase space dimension N = data.N; % nonzero entries in the multi-index array F_multi_pos = (n_mat ~= 0); sz = size(n_mat,2); col_pos = 1:sz;
Initialise space for the
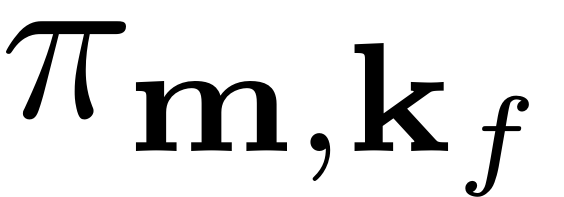 .
.
pis = zeros(size(col_pos,2),z_k);
The array
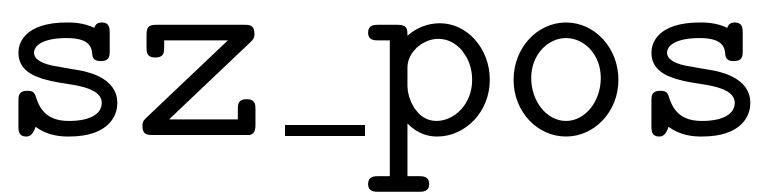 is a row vector containing in each row the number of nonzero entries
of the multi-index the row corresponds to. This is useful, since
is a row vector containing in each row the number of nonzero entries
of the multi-index the row corresponds to. This is useful, since
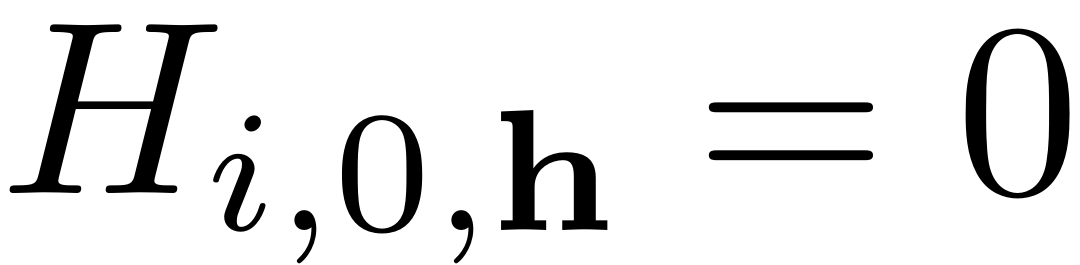 for any nonzero
for any nonzero
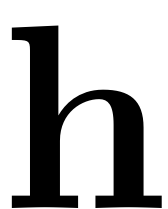 . Therefore for each
. Therefore for each
 in
in
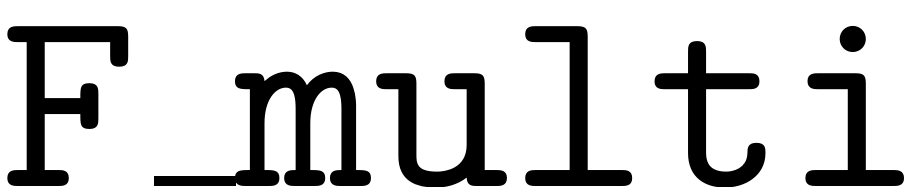 we only have to find the composition coefficients corresponding to
the nonzero entries of
we only have to find the composition coefficients corresponding to
the nonzero entries of
 . Furthermore then condition 1 looks like
. Furthermore then condition 1 looks like
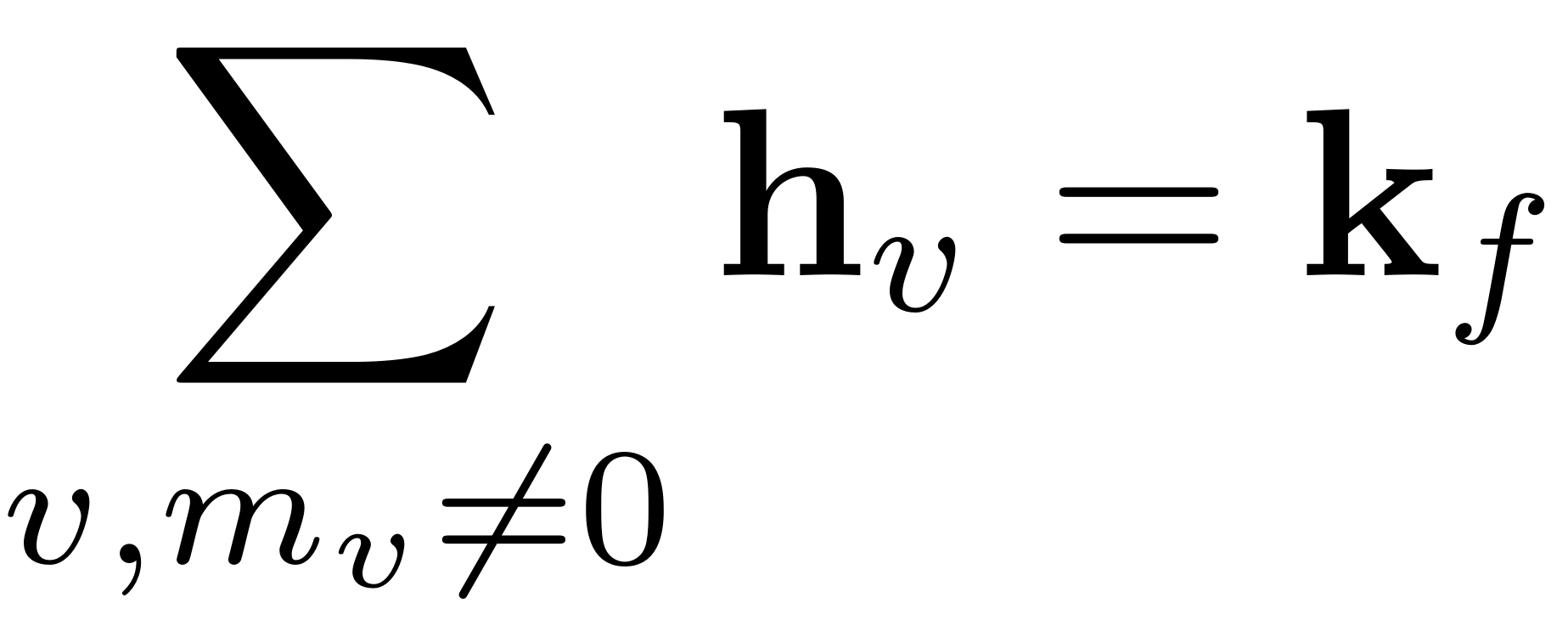 . For each
. For each
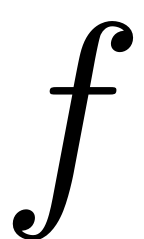 and
and
 all such combinations have to be found.
all such combinations have to be found.
sz_pos = sum(F_multi_pos,1);
This function computes all those combinations for all order
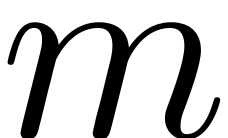 multi-indices
multi-indices
 and all
and all
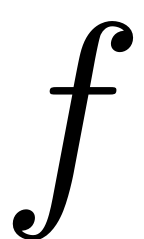 . It does so by considering unique numbers in
. It does so by considering unique numbers in
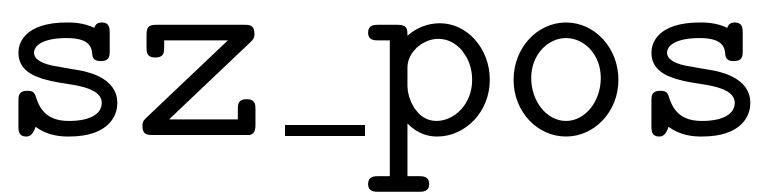 and using them as the number of multi-indices
and using them as the number of multi-indices
 that have to sum up to
that have to sum up to
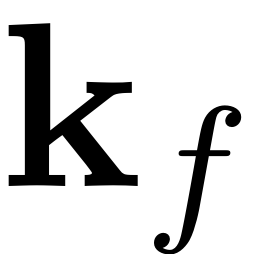 for all
for all
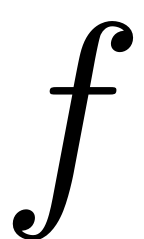 .
.
 is a cell array, that contains in its first dimension the
combinations for all
is a cell array, that contains in its first dimension the
combinations for all
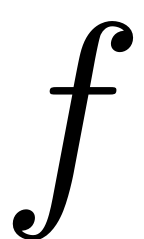 and its second dimension corresponds to unique numbers in
and its second dimension corresponds to unique numbers in
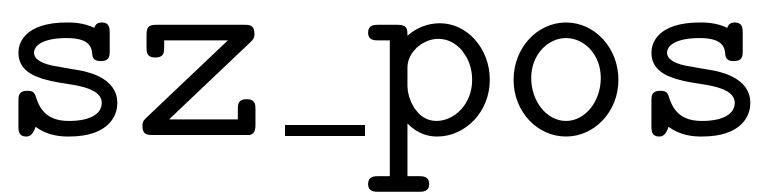 . They are stored in
. They are stored in
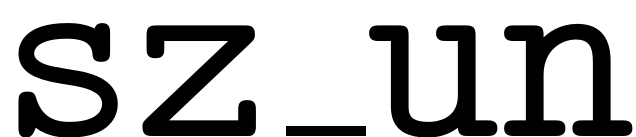 . For each entry in
. For each entry in
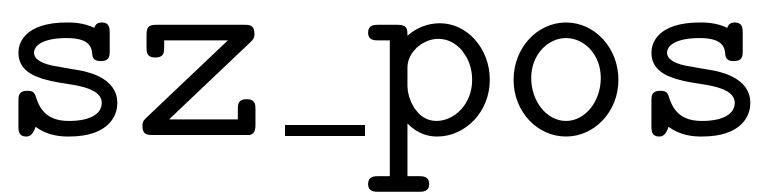 the corresponding entry in
the corresponding entry in
 gives the column that it corresponds to in
gives the column that it corresponds to in
 .
.
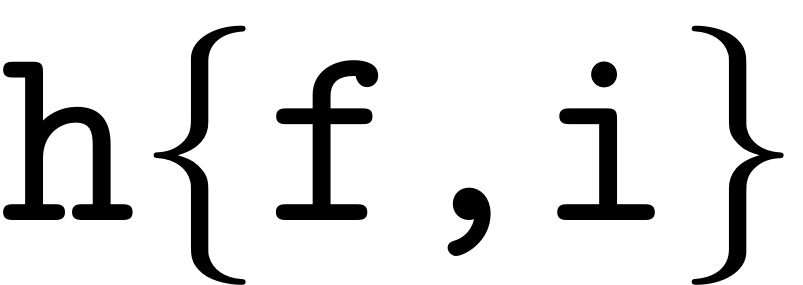 contains a 3 dimensional array. The first dimension has size
contains a 3 dimensional array. The first dimension has size
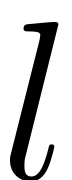 , the second hase size
, the second hase size
 . Its third dimension has size
. Its third dimension has size
 .
.
This array contains in every matrix a set
 that fulfills condition 1 for
that fulfills condition 1 for
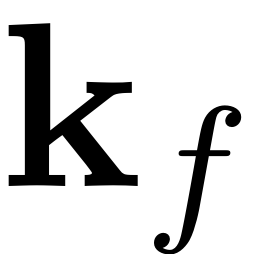 that is stored in
that is stored in
 . Each set consists of
. Each set consists of
 elements.
elements.
 contains the amount of combinations that exist for every tuple
contains the amount of combinations that exist for every tuple
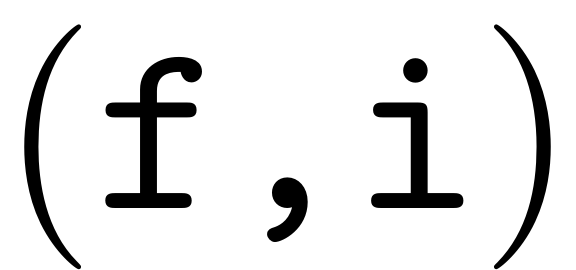 .
.
[h, combnos,sz_un,sz_un_ic] = multi_nsumk(sz_pos,K); %stores the order of all the multi-indices in h h_abs = cellfun(@(x) reshape(sum(x,1),size(x,2),[]), h, 'UniformOutput',false); %loop over all the order k multi-indices with index below center %index in conjugate ordering for f = 1:z_k %loop over unique amounts of nonzero entries in the %multi-indices m for i = 1:size(sz_un,2)
%position of multi-indices in F_multi that have sz_un(i) nonzero entries idx = sz_un_ic == i; %number of multi-indices in F_multi that have i nonzero entries sumidx = sum(idx); if sz_un(i) == 0 if nnz(K(:,f)) == 0 pis(idx,f) = ones(sumidx,1); end continue end %columns of Fm that contain i nonzero elements n_idx = n_mat(:,idx.'); n_idx_find = find(n_idx); [n_idx_row,~] = ind2sub(size(n_idx),n_idx_find);
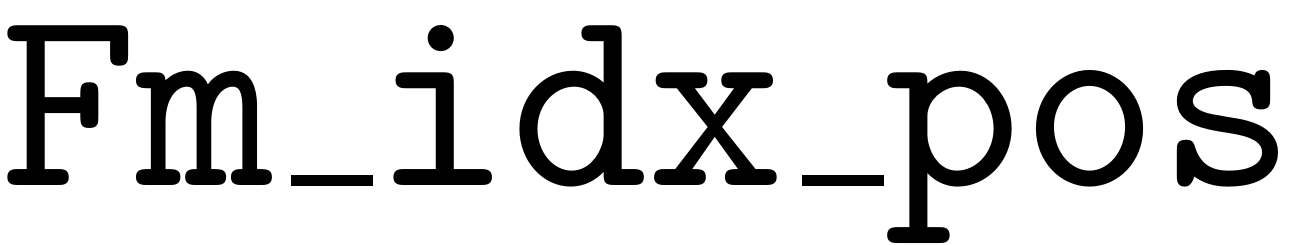 contains the entries of
contains the entries of
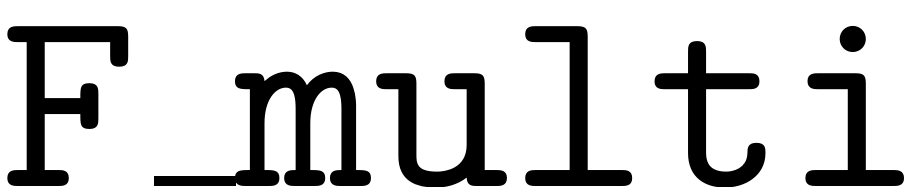 that correspond to the multi-indices that have
that correspond to the multi-indices that have
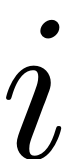 nonzero elements. It is therefore a
nonzero elements. It is therefore a
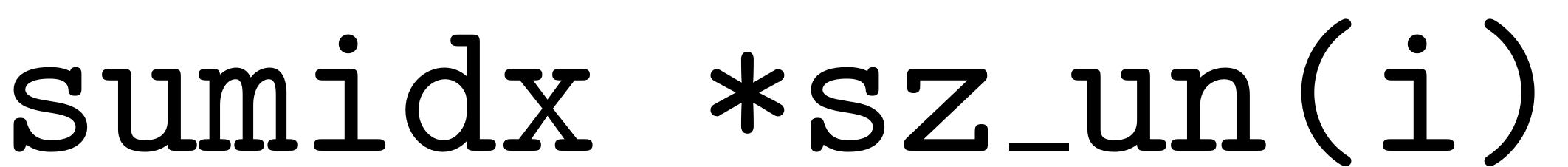 by 1 array.
by 1 array.
n_idx_pos = n_idx(n_idx_find);
This step checks where condition 2 is fulfilled.
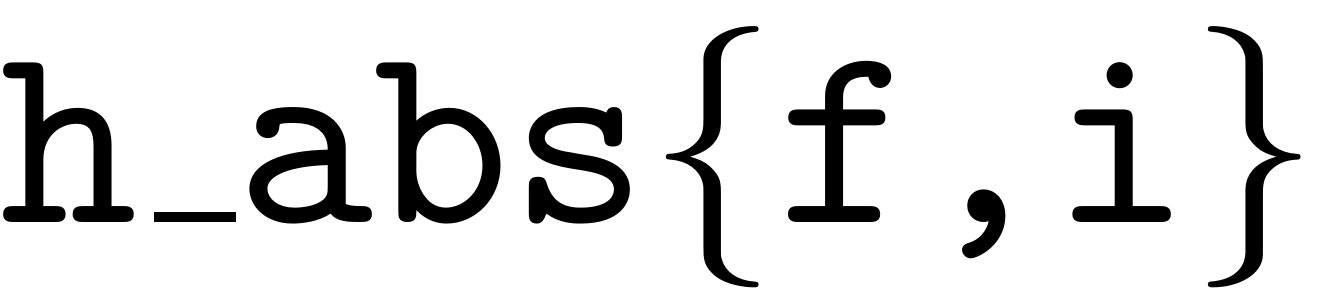 contains a
contains a
 by
by
 dimensionaly array. In every column it contains the absolute values
of all multi_indices of one combination
dimensionaly array. In every column it contains the absolute values
of all multi_indices of one combination
 that fulfills condition 1 for
that fulfills condition 1 for
 and contains
and contains
 elements. Condition 2 is checked simultaneously for all
elements. Condition 2 is checked simultaneously for all
 of order
of order
 that contain
that contain
 nonzero entries.
nonzero entries.
And therefore if the size
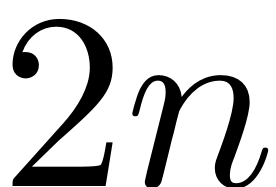 multi indices that have
multi indices that have
 nonzero elements are
nonzero elements are
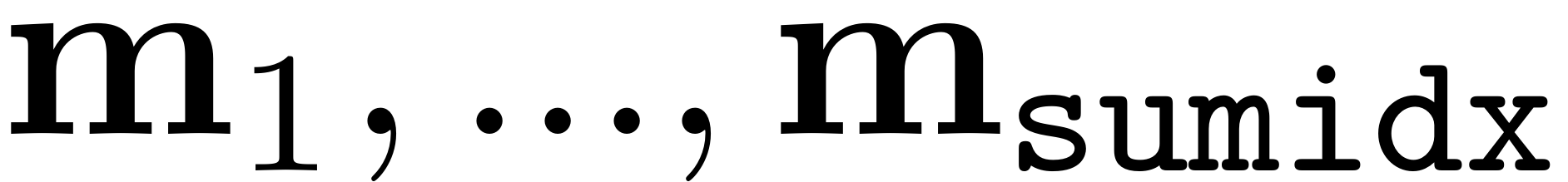 , and we define
, and we define
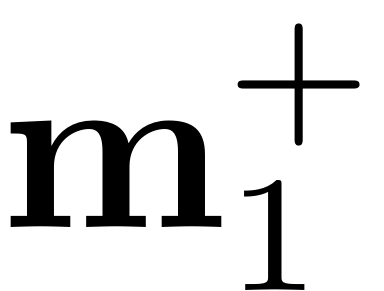 as the size
as the size
 multi-index containing the nonzero elements of
multi-index containing the nonzero elements of
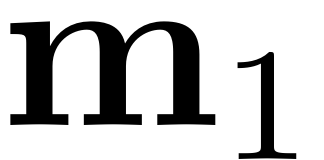 ,then condition 2 is checked.
,then condition 2 is checked.
Cond_dum = repmat(h_abs{f,i},sumidx,1) >= full(n_idx_pos);
Now we would like to check which combinations fulfill condition 2
for all of their elements. This corresponds to columns of
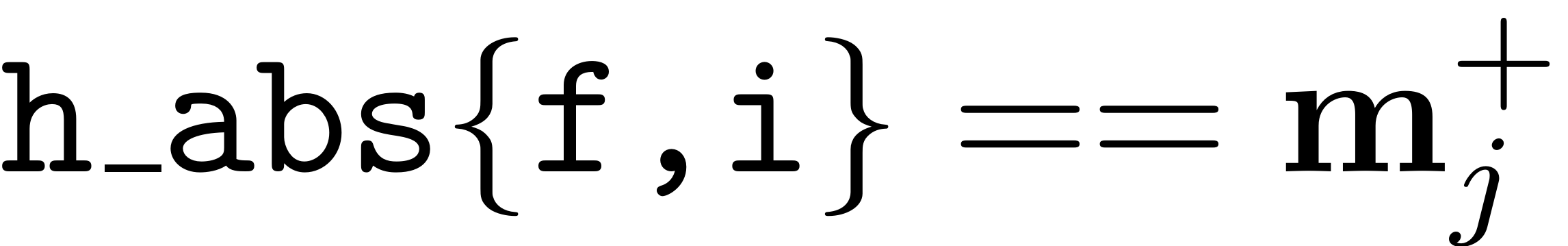 where all elements are one. So summing over the rows only the
columns that have
where all elements are one. So summing over the rows only the
columns that have
 as their entry correspond to valid combinations that fulfill
condition 2to for
as their entry correspond to valid combinations that fulfill
condition 2to for
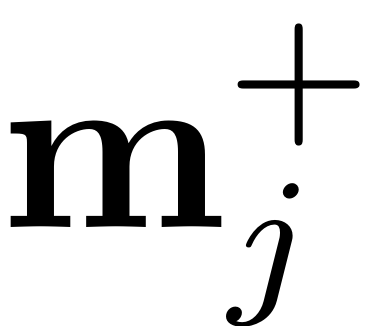 , and this has to be done for
, and this has to be done for
 .
.
To do this we transpose
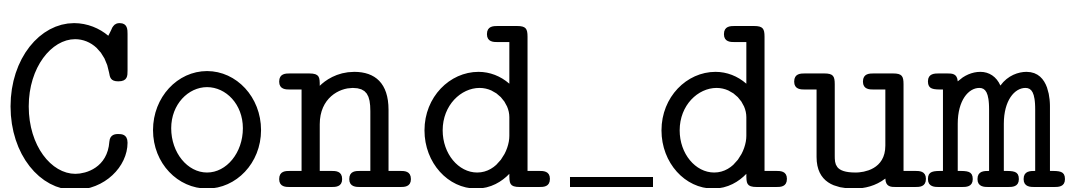 and permute the first two dimensions. Furthermore, now a third
dimension is added which each corresponds to one
and permute the first two dimensions. Furthermore, now a third
dimension is added which each corresponds to one
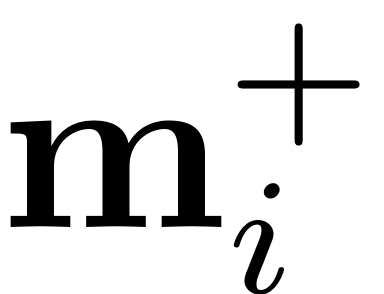 .
.
%reshape, such that every slice of 3rd dim corresponds to %conditions for one m, first dimension Cond_dum = reshape(Cond_dum.',[],sz_un(i),sumidx); %permute, every column now contains conds for one combo of %h_is, sum all those cond values, if they are all one in a %column, they contribute. Cond_dum = sum(permute( Cond_dum,[2,1,3]),1);
Now a slice of the third dimension looks like
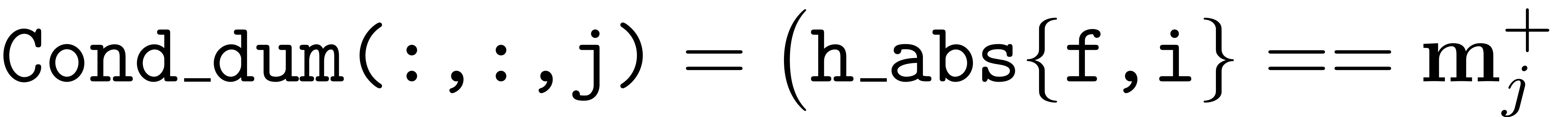 . The sum over the rows reveals which combos contribute. The
resulting vector is recast, such that every column corresponds to
one
. The sum over the rows reveals which combos contribute. The
resulting vector is recast, such that every column corresponds to
one
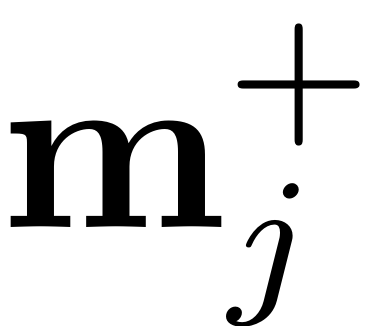 and the rows correspond to the combinations that fulfill condition
1. The ones that also fulfill condition 2 are logical ones, the
others are zero.
and the rows correspond to the combinations that fulfill condition
1. The ones that also fulfill condition 2 are logical ones, the
others are zero.
%check if every vector of a combo fulfills cond, if not %discard it Cond = sparse(reshape(Cond_dum == full(sz_un(i)),combnos(f,i),[] )); if nnz(Cond)==0 continue end
The array indices reads out the index of the valid combinations.
Specifically if the different combinations are numbered with numbers
1 to
 , then it assigns every valid combination the number it corresponds
to.
, then it assigns every valid combination the number it corresponds
to.
%contains indices to read out the ones fulfilling cond2 %from h indices = repmat([1:combnos(f,i)].',1,sumidx); Cond_ind = indices(Cond);
Consequently all valid combinations of multi-indices are explicitly
read out into a array that contains all of the multi-indices in its
second dimension. All valid combinations for
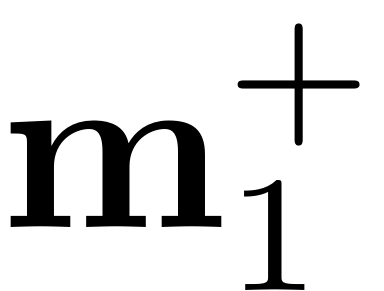 are in it as a sequence, followed by all valid combinations for
are in it as a sequence, followed by all valid combinations for
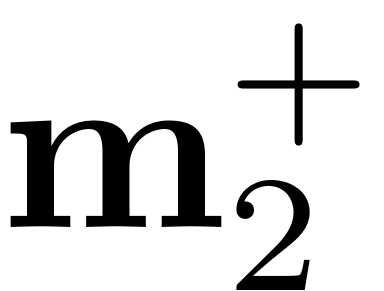 and so forth.
and so forth.
%All combos in first dim. each combo has nns(ind) %contributions - to get back, reshape to l, nns(ind), [] h_i = reshape( h{f,i}(:,:,reshape(Cond_ind,[],1)) ,l,[]);
In order to read out the composition coefficients corresponding to
all those multi-indices we have to know their position in a set of
reverse lexicographical ordering of all multi-indices of their
respective order and size. In order to do this efficient, unique
multi-indices are extracted from
 , and their position is calculated, in either conjugate ordering
(real system) or in reverse lex. ordering (non real system). Then
the subindices of all multi-indices are stored in the array
, and their position is calculated, in either conjugate ordering
(real system) or in reverse lex. ordering (non real system). Then
the subindices of all multi-indices are stored in the array
 .
.
[Cond_ind_un,~,Cond_ind_idx] = unique(Cond_ind);
h_i_combo = reshape(h{f,i}(:,:,Cond_ind_un),l,[]);
% Unique multi-indices that appear in these unique combinations
% h_i_combo_ic denotes position of the unique multi-idcs in the array of
% multi-idcs of unique combinations given by h_i_combo
[h_i_un,~,h_i_combo_ic] = unique(h_i_combo.','rows');
% Index of multi-idcs in the unique multi-idcs
h_i_idx_tmp = multi_index_2_ordering(h_i_un.','revlex',[]);
% Index of multi-idcs in the array of unique multi-idx combinations
% h_i_combo
h_i_combo_idx = h_i_idx_tmp(h_i_combo_ic);
% Reshape array of Index such that each row corresponds to all positions in
% one combination
h_i_combo_idx = reshape(h_i_combo_idx, i ,[]);
% Map the Index combinations to full set of non-unique combinations
h_i_idx = reshape(h_i_combo_idx(:,Cond_ind_idx),1,[]);
% Map unique multi-indices back to full multi-idcs
h_i_ic = reshape(h_i_combo_ic,i,[]);
h_i_ic = reshape(h_i_ic(:,Cond_ind_idx),[],1);
To read out the composition coefficients at the right order the
absolute values of the multi-indices also has to be known. They are
stored in
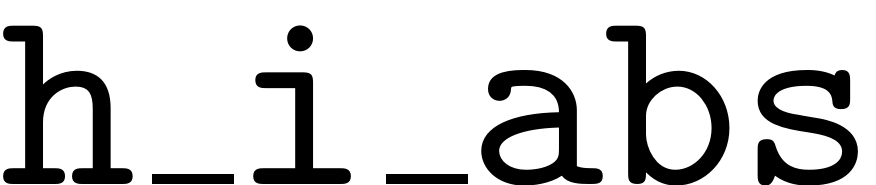 .
.
if l > 1 h_i_abs = sum(h_i_un.'); else h_i_abs = h_i_un.'; end [h_i_abs_un,~,h_i_abs_ic] = unique(h_i_abs);
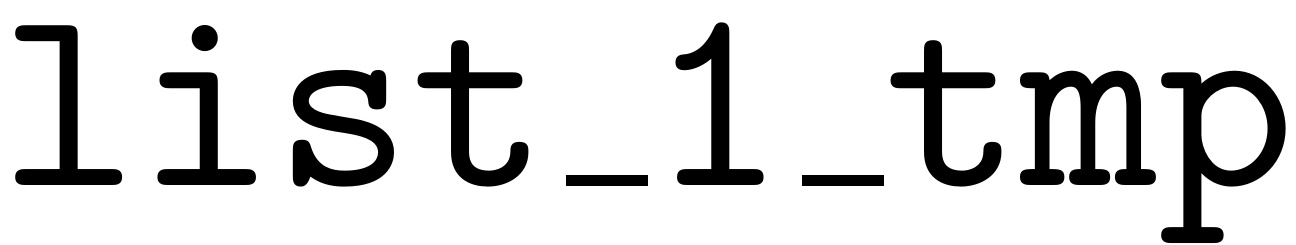 contains the positions of the nonzero elements of all the
multi-indices
contains the positions of the nonzero elements of all the
multi-indices
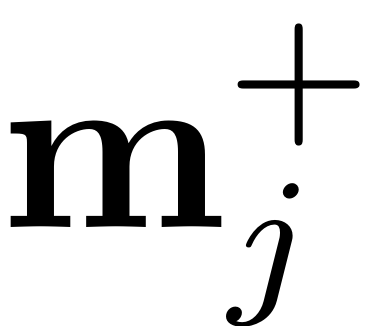 in column
in column
 . Then each column is replicated by the amount of combinations that
fulfill both condition 1 and condition 2, which is given by
. Then each column is replicated by the amount of combinations that
fulfill both condition 1 and condition 2, which is given by
 , since
, since
 contains in column
contains in column
 and row
and row
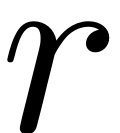 logical indices that indicate wheter combination
logical indices that indicate wheter combination
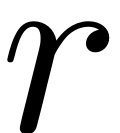 fulfills both conditions for
fulfills both conditions for
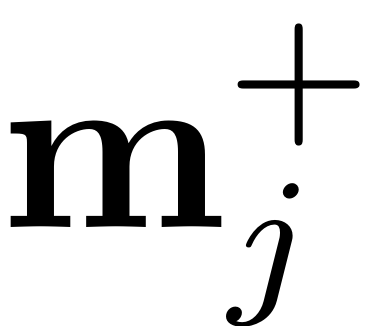 . That is then reshaped, such that the entry
. That is then reshaped, such that the entry
 in
in
 contains the index
contains the index
 of the composition coefficient
of the composition coefficient
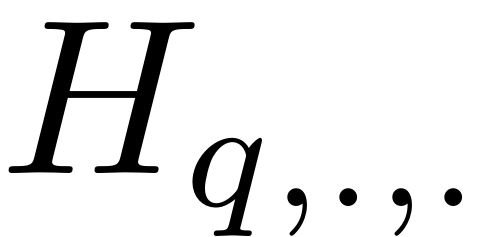 that the multi-index in position
that the multi-index in position
 in
in
 corresponds to.
corresponds to.
%contains the row index for all of the valid combos for %all ms in the same ordering as in HV list_1_tmp = reshape(n_idx_row,sz_un(i),[]); list_1 = reshape(repelem(list_1_tmp,1,sum(Cond,1)),1,[] );
The same thing is done for the entries (not the positions) of all
the multi-indices
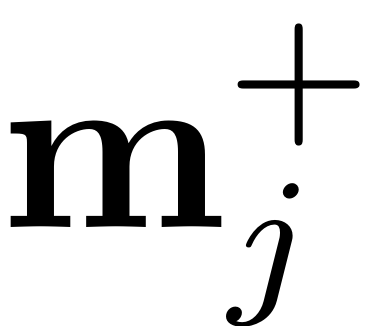 . The entry
. The entry
 in
in
 contains the value
contains the value
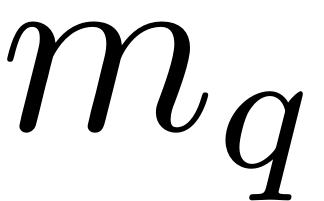 of the composition coefficient
of the composition coefficient
 that the multi-index in position
that the multi-index in position
 in
in
 corresponds to.
corresponds to.
%contains the entries of m for the valid combos for %all ms in the same ordering as in HV list_2_tmp = reshape(n_idx_pos,sz_un(i),[]); list_2 = reshape(repelem(list_2_tmp,1,sum(Cond,1)),1,[]);
What is left now is to multiply and add the indices accordingly to
get the right force contribution. Firstly all the composition
coefficients are ready out into
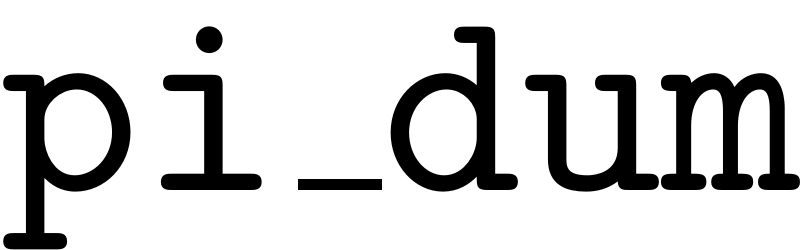 .
.
pi_dum = ones(size(h_i,2),1);
run_ord = 1;
for ord = h_i_abs_un
The logical index
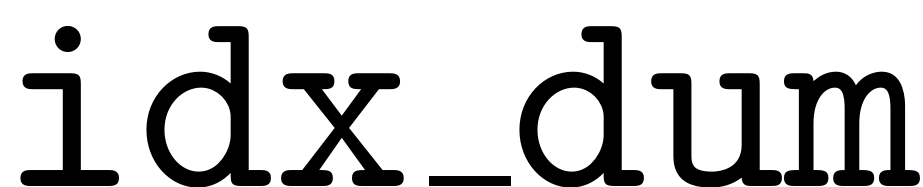 contains the positions of all multi-indices in
contains the positions of all multi-indices in
 that have order
that have order
 . The explicit positions of them are stored in
. The explicit positions of them are stored in
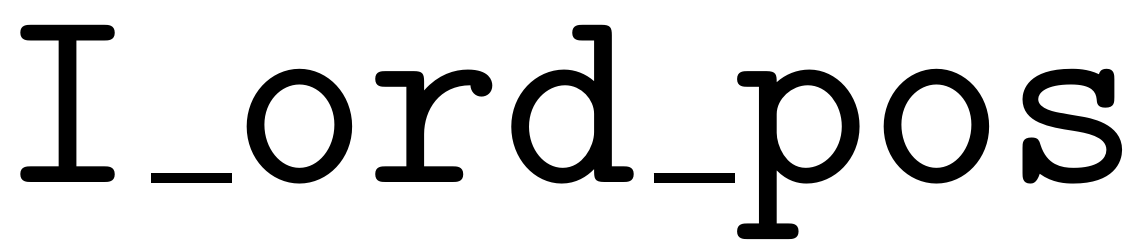 .
.
idx_dum = 1:size(h_i_abs_ic.',2);
idx_dum = idx_dum(h_i_abs_ic.' == run_ord);
idx_dum = (h_i_ic == idx_dum);
idx_dum = sum(idx_dum,2);
I_ord = logical(idx_dum);
The values corresponding to those multi_indices of order
 are read out of the arrays that specify the position of the
composition coefficients for each of the multi-indices, being the
phase space direction they correspond to, the multi-index subindex
in the reverse lexicographically ordered set they have and the
multi-index entry of the multi-index
are read out of the arrays that specify the position of the
composition coefficients for each of the multi-indices, being the
phase space direction they correspond to, the multi-index subindex
in the reverse lexicographically ordered set they have and the
multi-index entry of the multi-index
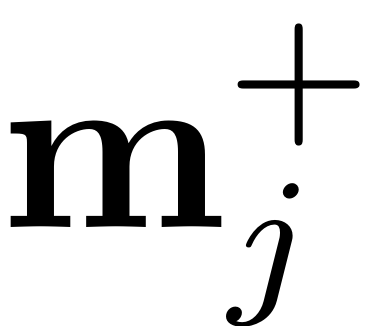 they correspond to.
they correspond to.
I_1 = list_1(I_ord);
I_2 = h_i_idx(I_ord);
I_3 = list_2(I_ord);
In order to make use of the symmetry of the SSM-coefficients, all the multi-indices that in conjugate ordering have subindex bigger than the conjugate center index are changed to their conjugate counterpart, and for them then conjugate composition coefficients corresponding to this conjugate multi-index are read out.
z_ord = nchoosek(ord+l-1,l-1);
%split in the two index parts about conjugate
%center index at order ord
lin_idx = sub2ind([N,z_ord,ord],I_1,I_2,I_3);
pi_dum(I_ord) = data.H{ord}(lin_idx);
run_ord = run_ord +1;
end
The following step multiplies all composition coefficients that correspond to one combination of multi-indices fulfilling condition 1 and 2.
%multiplication
pi_dum = prod(reshape(pi_dum, sz_un(i),[]),1);
Next all the values of
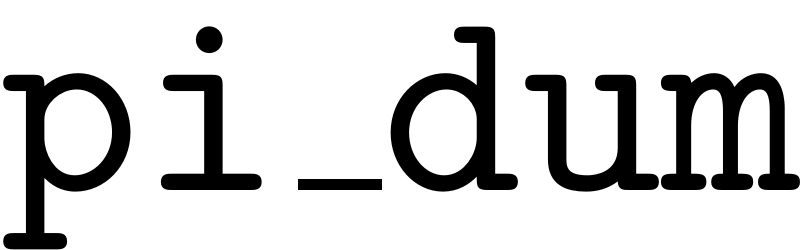 corresponding to the same multi-index
corresponding to the same multi-index
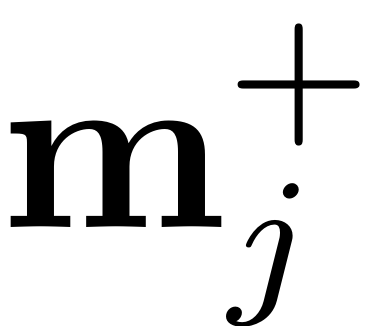 have to be added. This is done by creating an array
have to be added. This is done by creating an array
 that contains for each entry in
that contains for each entry in
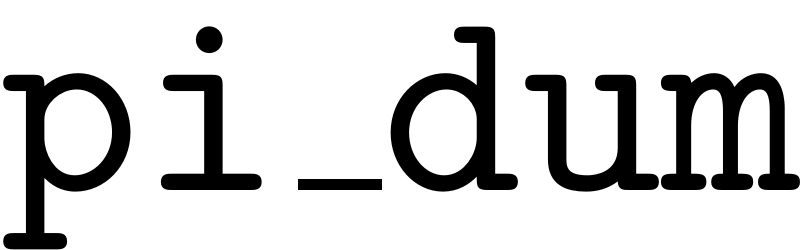 the index
the index
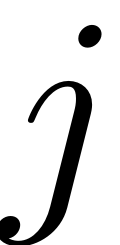 of the size
of the size
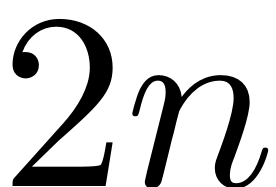 multi-index it corresponds to. Using
multi-index it corresponds to. Using
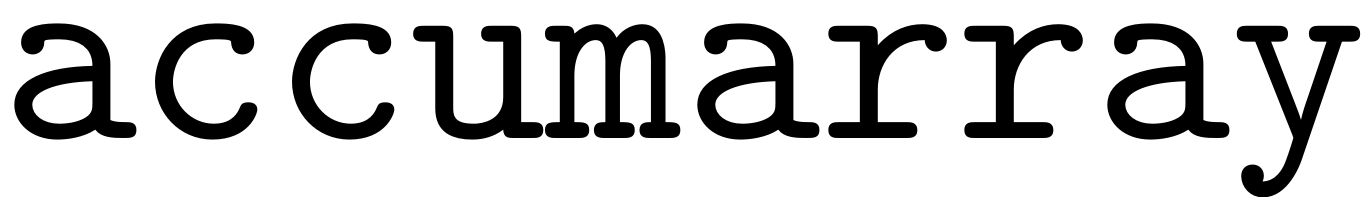 the values that correspond to the same index
the values that correspond to the same index
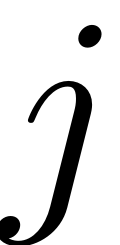 are added up and then stored in the array
are added up and then stored in the array
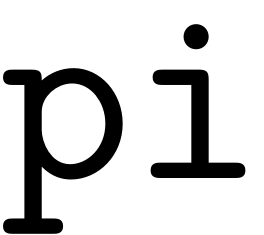 that contains all the composition terms.
that contains all the composition terms.
%sum over combos and put into position list_3 = repelem([1:sumidx].',sum(Cond,1)); % Indices to read out the contributions into correct position n_contrib = sum(Cond,1)>0; idx_pos = find(idx); accum_pi = accumarray(reshape(list_3,[],1),pi_dum); pis(idx_pos(n_contrib),f) = accum_pi(find(n_contrib));
end end
end function [pis] = pi_nk_conj(F_multi,K,data)
% Conjugate center index at all orders, for % imaginary system this is empty since then no symmetry is % inherent and we only need the number of multi-indices that % exist at order k, given by nchoosek(k+l-1,l-1) k = sum(K(:,1),1); % Order of computation Z_cci = data.Z_cci; z_k = Z_cci(k); l = size(K,1); % SSM dimension % Phase space dimension N = data.N; % if system is not real, then full set of order k multi-indices in reverse lex. ordering revlex2conj = data.revlex2conj; % Set to convert indices from rev. lex. to conjugate ordering % nonzero entries in the multi-index array F_multi_pos = (F_multi ~= 0); sz = size(F_multi,2); col_pos = 1:sz;
Initialise space for the
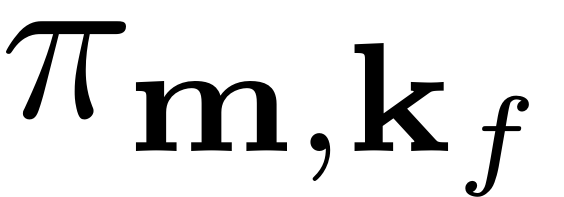 .
.
pis = zeros(size(col_pos,2),z_k);
The array
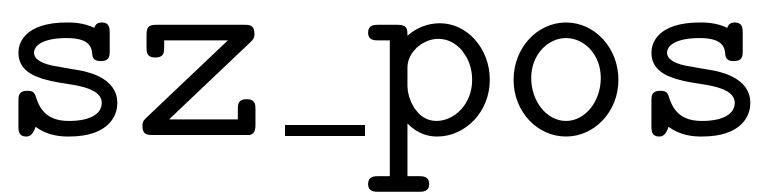 is a row vector containing in each row the number of nonzero entries
of the multi-index the row corresponds to. This is useful, since
is a row vector containing in each row the number of nonzero entries
of the multi-index the row corresponds to. This is useful, since
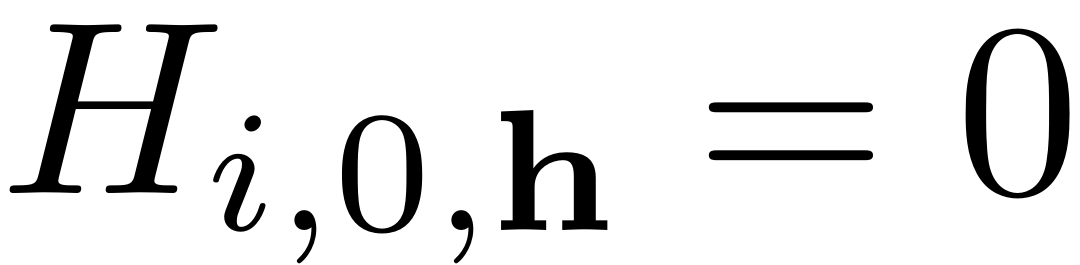 for any nonzero
for any nonzero
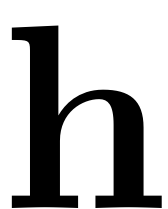 . Therefore for each
. Therefore for each
 in
in
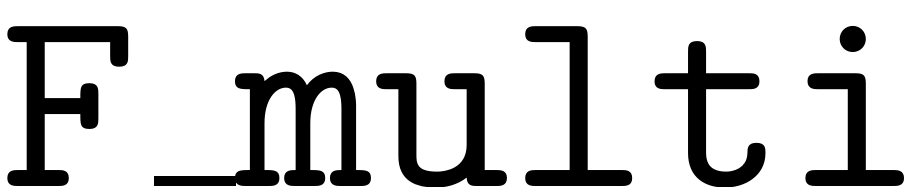 we only have to find the composition coefficients corresponding to
the nonzero entries of
we only have to find the composition coefficients corresponding to
the nonzero entries of
 . Furthermore then condition 1 looks like
. Furthermore then condition 1 looks like
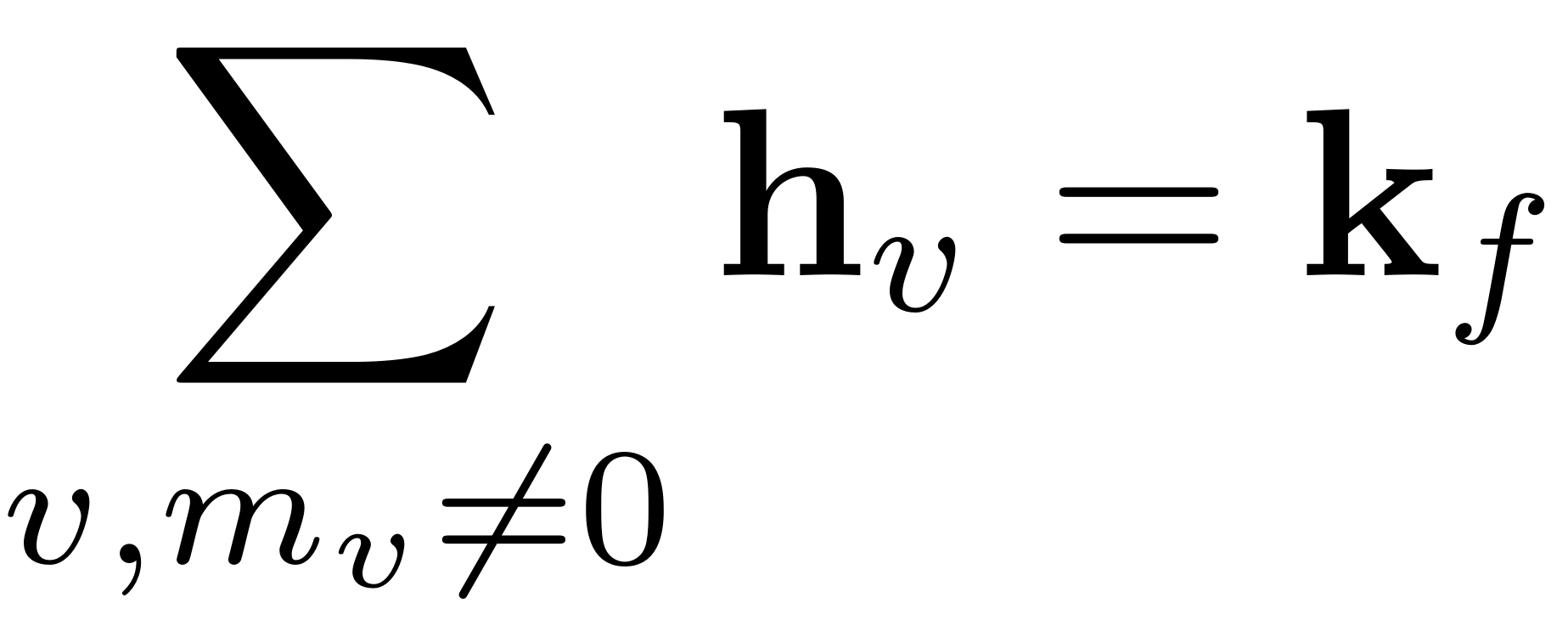 . For each
. For each
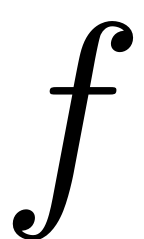 and
and
 all such combinations have to be found.
all such combinations have to be found.
sz_pos = sum(F_multi_pos,1);
This function computes all those combinations for all order
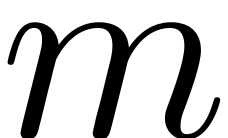 multi-indices
multi-indices
 and all
and all
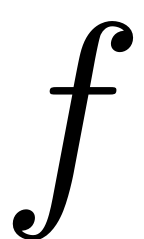 . It does so by considering unique numbers in
. It does so by considering unique numbers in
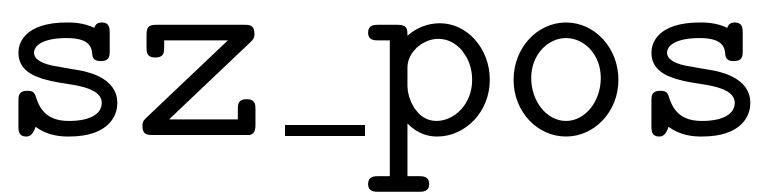 and using them as the number of multi-indices
and using them as the number of multi-indices
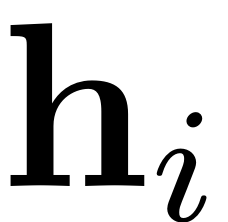 that have to sum up to
that have to sum up to
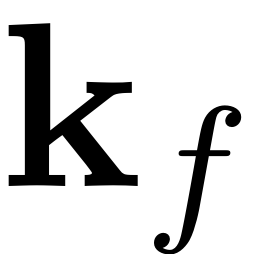 for all
for all
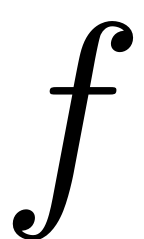 .
.
 is a cell array, that contains in its first dimension the
combinations for all
is a cell array, that contains in its first dimension the
combinations for all
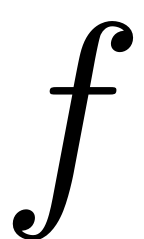 and its second dimension corresponds to unique numbers in
and its second dimension corresponds to unique numbers in
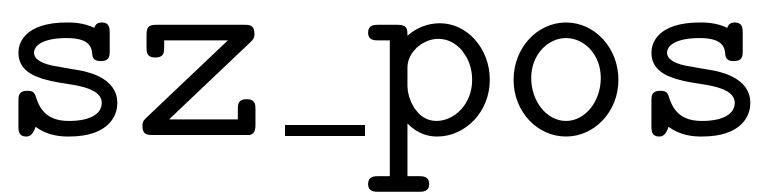 . They are stored in
. They are stored in
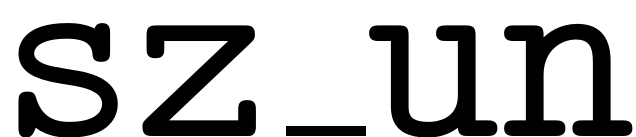 . For each entry in
. For each entry in
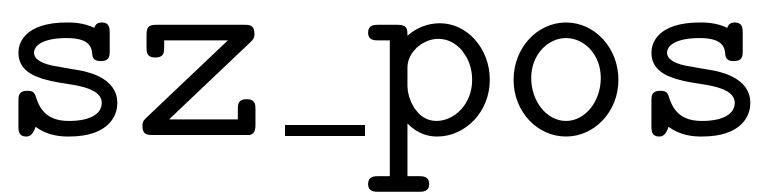 the corresponding entry in
the corresponding entry in
 gives the column that it corresponds to in
gives the column that it corresponds to in
 .
.
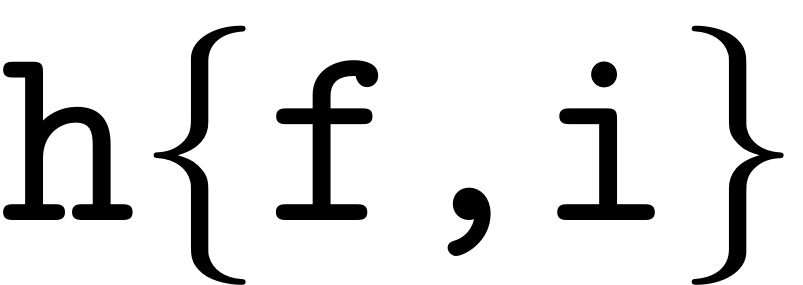 contains a 3 dimensional array. The first dimension has size
contains a 3 dimensional array. The first dimension has size
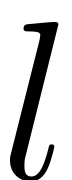 , the second hase size
, the second hase size
 . Its third dimension has size
. Its third dimension has size
 .
.
This array contains in every matrix a set
 that fulfills condition 1 for
that fulfills condition 1 for
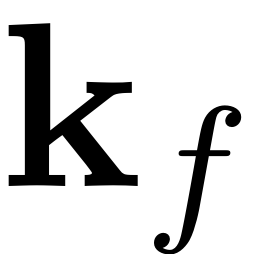 that is stored in
that is stored in
 . Each set consists of
. Each set consists of
 elements.
elements.
 contains the amount of combinations that exist for every tuple
contains the amount of combinations that exist for every tuple
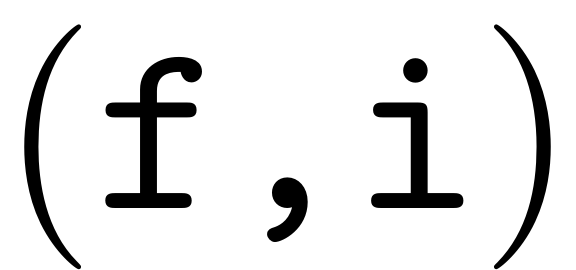 .
.
[h, combnos,sz_un,sz_un_ic] = multi_nsumk(sz_pos,K,'remove_trivial_idcs'); %stores the order of all the multi-indices in h h_abs = cellfun(@(x) reshape(sum(x,1),size(x,2),[]), h, 'UniformOutput',false); %loop over all the order k multi-indices with index below center %index in conjugate ordering for f = 1:z_k %loop over unique amounts of nonzero entries in the %multi-indices m for i = 1:size(sz_un,2)
%position of multi-indices in F_multi that have sz_un(i) nonzero entries idx = sz_un_ic == i; %number of multi-indices in F_multi that have i nonzero entries sumidx = sum(idx); %columns of Fm that contain i nonzero elements Fm_idx = F_multi(:,idx.'); Fm_idx_find = find(Fm_idx); [Fm_idx_row,~] = ind2sub(size(Fm_idx),Fm_idx_find);
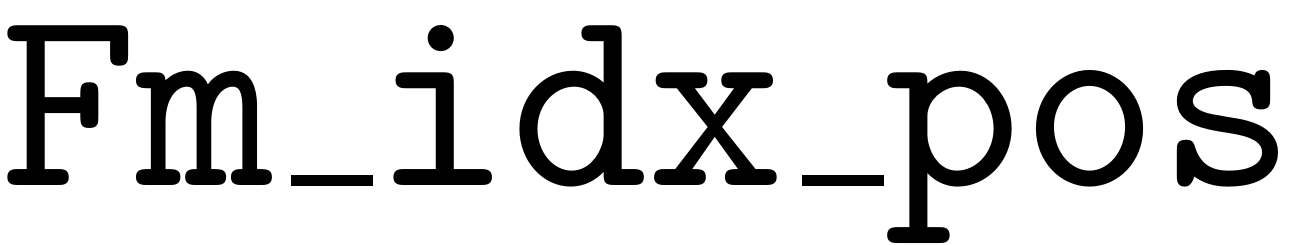 contains the entries of
contains the entries of
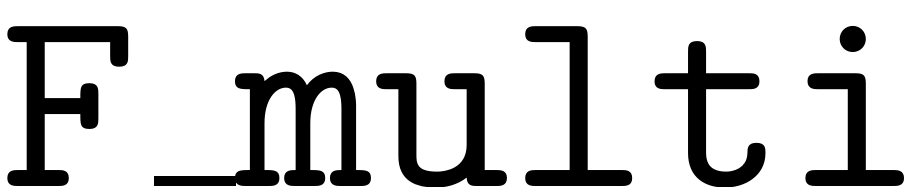 that correspond to the multi-indices that have
that correspond to the multi-indices that have
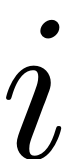 nonzero elements. It is therefore a
nonzero elements. It is therefore a
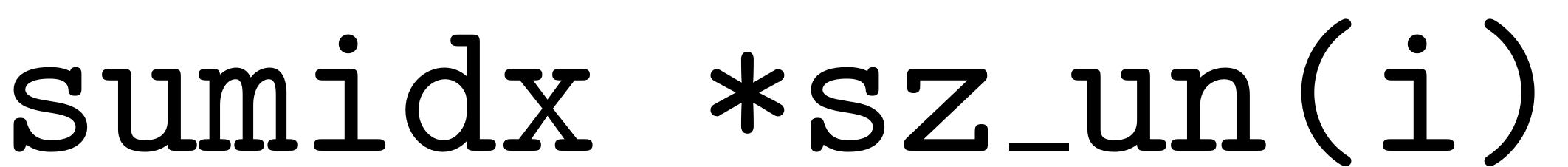 by 1 array.
by 1 array.
Fm_idx_pos = Fm_idx(Fm_idx_find);
This step checks where condition 2 is fulfilled.
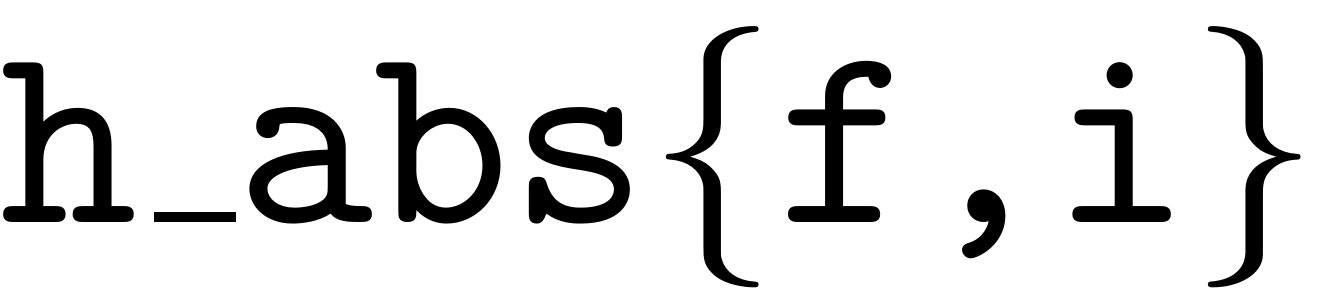 contains a
contains a
 by
by
 dimensionaly array. In every column it contains the absolute values
of all multi_indices of one combination
dimensionaly array. In every column it contains the absolute values
of all multi_indices of one combination
 that fulfills condition 1 for
that fulfills condition 1 for
 and contains
and contains
 elements. Condition 2 is checked simultaneously for all
elements. Condition 2 is checked simultaneously for all
 of order
of order
 that contain
that contain
 nonzero entries.
nonzero entries.
And therefore if the size
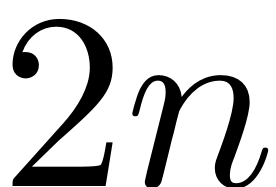 multi indices that have
multi indices that have
 nonzero elements are
nonzero elements are
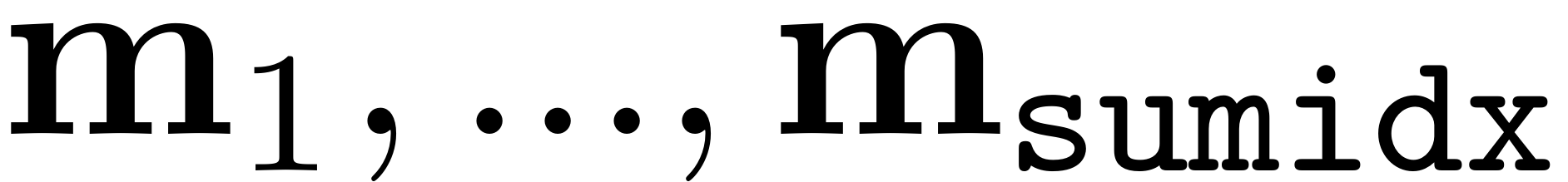 , and we define
, and we define
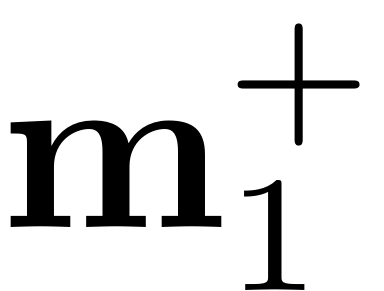 as the size
as the size
 multi-index containing the nonzero elements of
multi-index containing the nonzero elements of
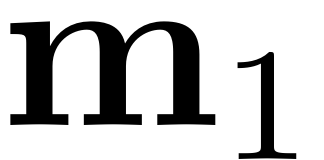 ,then condition 2 is
,then condition 2 is
Cond_dum = repmat(h_abs{f,i},sumidx,1) >= full(Fm_idx_pos);
Now we would like to check which combinations fulfill condition 2
for all of their elements. This corresponds to columns of
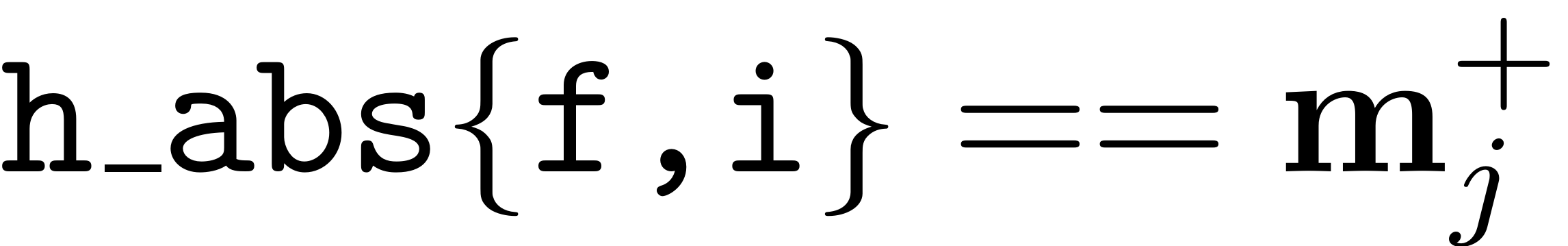 where all elements are one. So summing over the rows only the
columns that have
where all elements are one. So summing over the rows only the
columns that have
 as their entry correspond to valid combinations that fulfill
condition 2to for
as their entry correspond to valid combinations that fulfill
condition 2to for
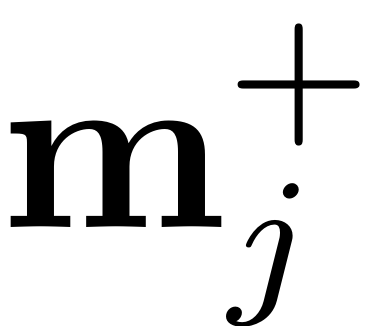 , and this has to be done for
, and this has to be done for
 .
.
To do this we transpose
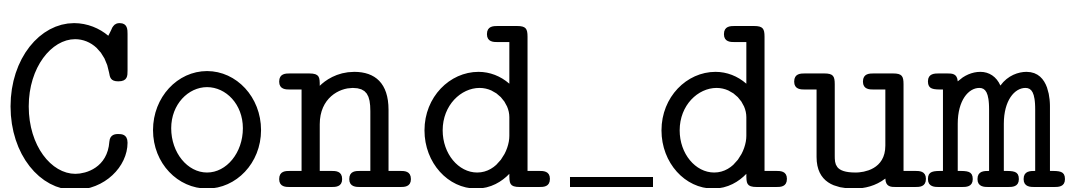 and permute the first two dimensions. Furthermore, now a third
dimension is added which each corresponds to one
and permute the first two dimensions. Furthermore, now a third
dimension is added which each corresponds to one
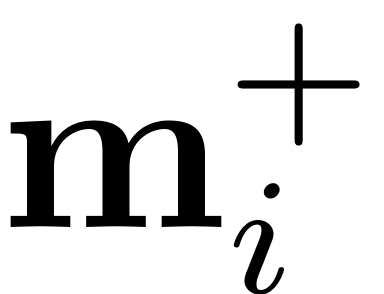 .
.
%reshape, such that every slice of 3rd dim corresponds to %conditions for one m, first dimension Cond_dum = reshape(Cond_dum.',[],sz_un(i),sumidx); %permute, every column now contains conds for one combo of %h_is, sum all those cond values, if they are all one in a %column, they contribute. Cond_dum = sum(permute( Cond_dum,[2,1,3]),1);
Now a slice of the third dimension looks like
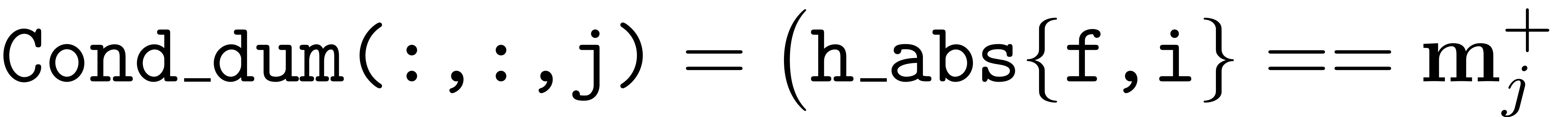 . The sum over the rows reveals which combos contribute. The
resulting vector is recast, such that every column corresponds to
one
. The sum over the rows reveals which combos contribute. The
resulting vector is recast, such that every column corresponds to
one
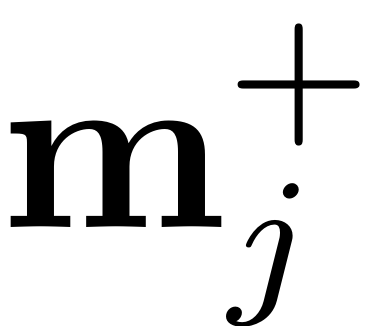 and the rows correspond to the combinations that fulfill condition
1. The ones that also fulfill condition 2 are logical ones, the
others are zero.
and the rows correspond to the combinations that fulfill condition
1. The ones that also fulfill condition 2 are logical ones, the
others are zero.
%check if every vector of a combo fulfills cond, if not %discard it Cond = reshape(Cond_dum == full(sz_un(i)),combnos(f,i),[] ); if nnz(Cond) == 0 continue end
The array indices reads out the index of the valid combinations.
Specifically if the different combinations are numbered with numbers
1 to
 , then it assigns every valid combination the number it corresponds
to.
, then it assigns every valid combination the number it corresponds
to.
%contains indices to read out the ones fulfilling cond2 %from h indices = repmat([1:combnos(f,i)].',1,sumidx); Cond_ind = indices(Cond);
Consequently all valid combinations of multi-indices are explicitly
read out into a array that contains all of the multi-indices in its
second dimension. All valid combinations for
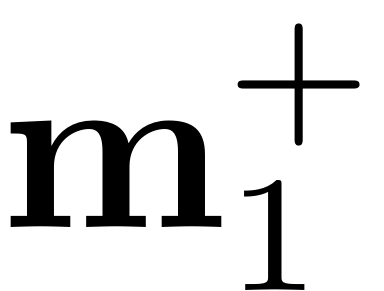 are in it as a sequence, followed by all valid combinations for
are in it as a sequence, followed by all valid combinations for
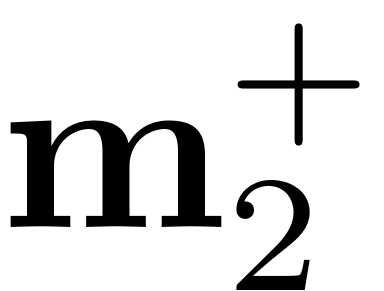 and so forth.
and so forth.
%All combos in first dim. each combo has nns(ind) %contributions - to get back, reshape to l, nns(ind), [] h_i = reshape( h{f,i}(:,:,reshape(Cond_ind,[],1)) ,l,[]);
In order to read out the composition coefficients corresponding to
all those multi-indices we have to know their position in a set of
reverse lexicographical ordering of all multi-indices of their
respective order and size. In order to do this efficient, unique
multi-indices are extracted from
 , and their position is calculated, in either conjugate ordering
(real system) or in reverse lex. ordering (non real system). Then
the subindices of all multi-indices are stored in the array
, and their position is calculated, in either conjugate ordering
(real system) or in reverse lex. ordering (non real system). Then
the subindices of all multi-indices are stored in the array
 . Unique combinations which fulfill the condition
. Unique combinations which fulfill the condition
[Cond_ind_un,~,Cond_ind_idx] = unique(Cond_ind);
h_i_combo = reshape(h{f,i}(:,:,Cond_ind_un),l,[]);
% Unique multi-indices that appear in these unique combinations
% h_i_combo_ic denotes position of the unique multi-idcs in the array of
% multi-idcs of unique combinations given by h_i_combo
[h_i_un,~,h_i_combo_ic] = unique(h_i_combo.','rows');
% Index of multi-idcs in the unique multi-idcs
h_i_idx_tmp = multi_index_2_ordering(h_i_un.',data.ordering,revlex2conj);
% Index of multi-idcs in the array of unique multi-idx combinations
% h_i_combo
h_i_combo_idx = h_i_idx_tmp(h_i_combo_ic);
% Reshape array of Index such that each row corresponds to all positions in
% one combination
h_i_combo_idx = reshape(h_i_combo_idx, i ,[]);
% Map the Index combinations to full set of non-unique combinations
h_i_idx = reshape(h_i_combo_idx(:,Cond_ind_idx),[],1);
% Map unique multi-indices back to full multi-idcs
h_i_ic = reshape(h_i_combo_ic,i,[]);
h_i_ic = reshape(h_i_ic(:,Cond_ind_idx),[],1);
%
To read out the composition coefficients at the right order the
absolute values of the multi-indices also has to be known. They are
stored in
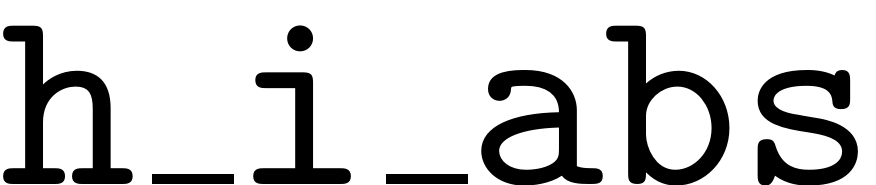 .
.
h_i_abs = sum(h_i_un.');
[h_i_abs_un,~,h_i_abs_ic] = unique(h_i_abs);
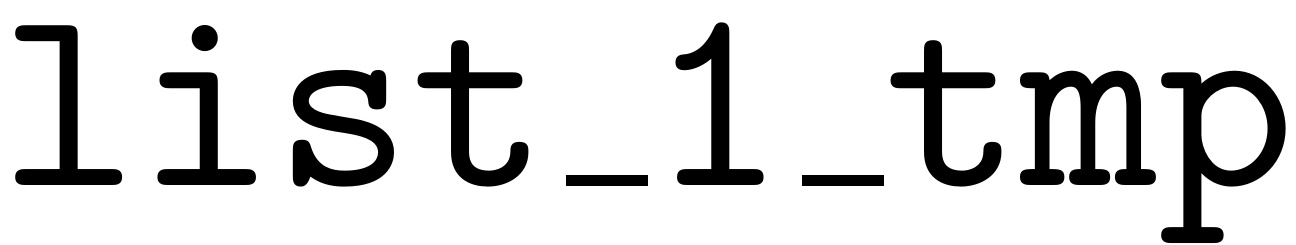 contains the positions of the nonzero elements of all the
multi-indices
contains the positions of the nonzero elements of all the
multi-indices
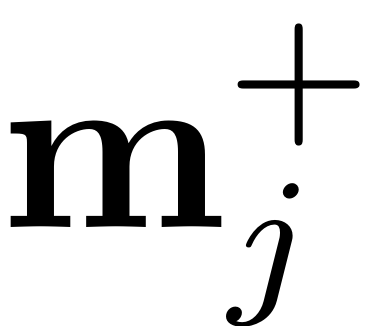 in column
in column
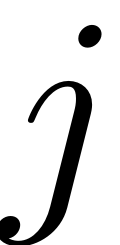 . Then each column is replicated by the amount of combinations that
fulfill both condition 1 and condition 2, which is given by
. Then each column is replicated by the amount of combinations that
fulfill both condition 1 and condition 2, which is given by
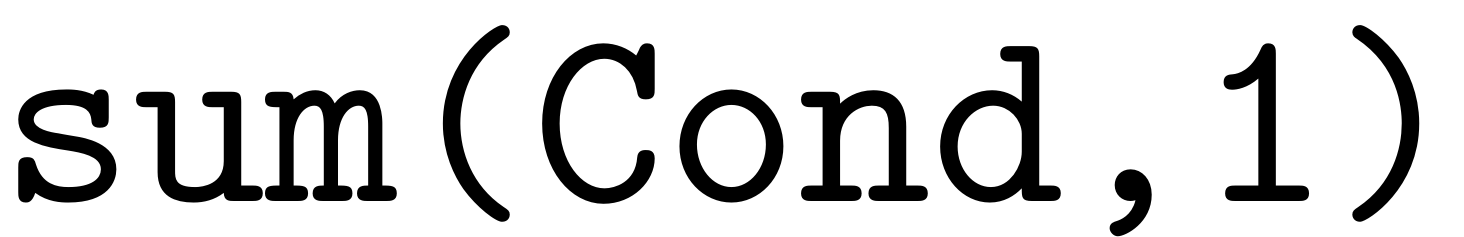 , since
, since
 contains in column
contains in column
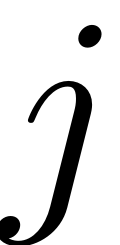 and row
and row
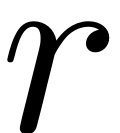 logical indices that indicate wheter combination
logical indices that indicate wheter combination
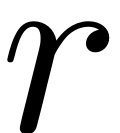 fulfills both conditions for
fulfills both conditions for
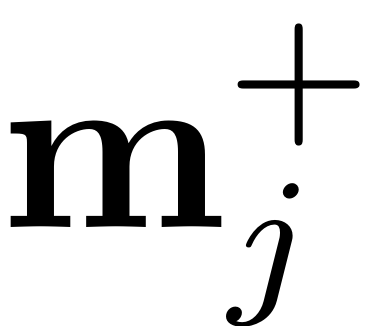 . That is then reshaped, such that the entry
. That is then reshaped, such that the entry
 in
in
 contains the index
contains the index
 of the composition coefficient
of the composition coefficient
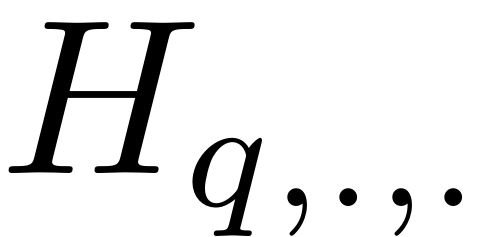 that the multi-index in position
that the multi-index in position
 in
in
 corresponds to.
corresponds to.
%contains the row index for all of the valid combos for %all ms in the same ordering as in HV list_1_tmp = reshape(Fm_idx_row,sz_un(i),[]); list_1 = reshape(repelem(list_1_tmp,1,sum(Cond,1)),[],1 );
The same thing is done for the entries (not the positions) of all
the multi-indices
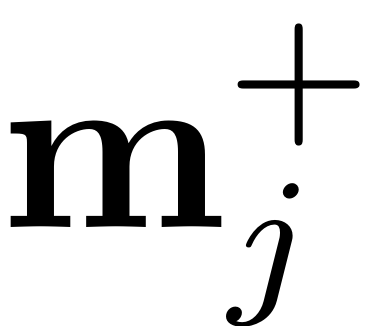 . The entry
. The entry
 in
in
 contains the value
contains the value
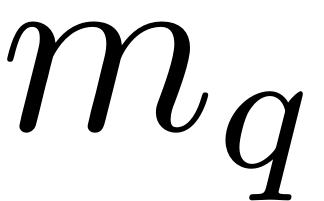 of the composition coefficient
of the composition coefficient
 that the multi-index in position
that the multi-index in position
 in
in
 corresponds to.
corresponds to.
%contains the entries of m for the valid combos for %all ms in the same ordering as in HV list_2_tmp = reshape(Fm_idx_pos,sz_un(i),[]); list_2 = reshape(repelem(list_2_tmp,1,sum(Cond,1)),[],1);
What is left now is to multiply and add the indices accordingly to
get the right force contribution. Firstly all the composition
coefficients are ready out into
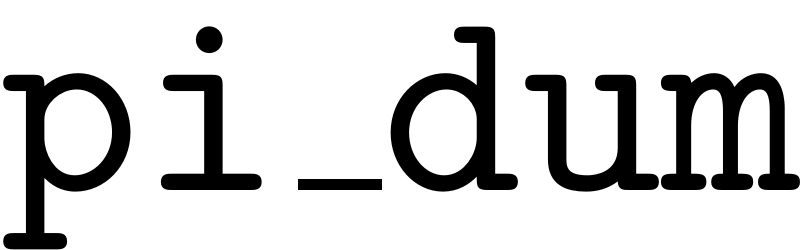 .
.
pi_dum = ones(size(h_i,2),1);
run_ord = 1;
for ord = h_i_abs_un
The logical index
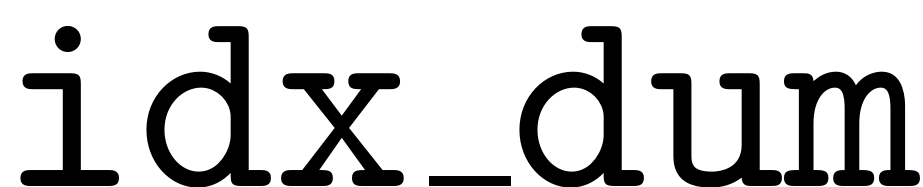 contains the positions of all multi-indices in
contains the positions of all multi-indices in
 that have order
that have order
 . The explicit positions of them are stored in
. The explicit positions of them are stored in
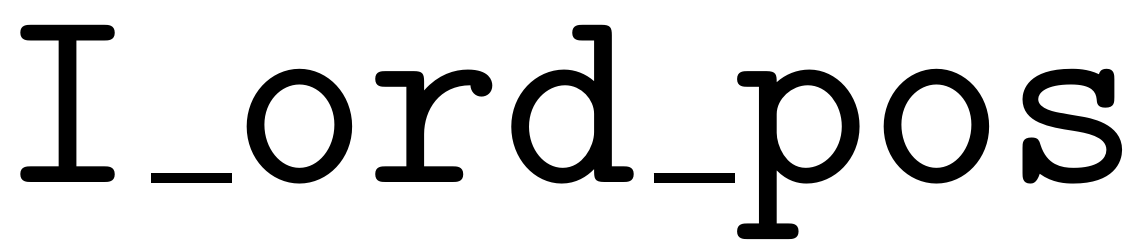 .
.
idx_dum = 1:size(h_i_abs_ic.',2);
idx_dum = idx_dum(h_i_abs_ic.' == run_ord);
idx_dum = (h_i_ic == idx_dum);
idx_dum = sum(idx_dum,2);
I_ord = logical(idx_dum);
I_ord_pos = find(I_ord);
The values corresponding to those multi_indices of order
 are read out of the arrays that specify the position of the
composition coefficients for each of the multi-indices, being the
phase space direction they correspond to, the multi-index subindex
in the reverse lexicographically ordered set they have and the
multi-index entry of the multi-index
are read out of the arrays that specify the position of the
composition coefficients for each of the multi-indices, being the
phase space direction they correspond to, the multi-index subindex
in the reverse lexicographically ordered set they have and the
multi-index entry of the multi-index
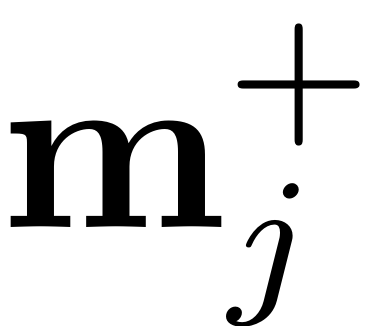 they correspond to.
they correspond to.
I_1 = list_1(I_ord);
I_2 = h_i_idx(I_ord);
I_3 = list_2(I_ord);
In order to make use of the symmetry of the SSM-coefficients, all the multi-indices that in conjugate ordering have subindex bigger than the conjugate center index are changed to their conjugate counterpart, and for them then conjugate composition coefficients corresponding to this conjugate multi-index are read out.
z_ord = nchoosek(ord+l-1,l-1);
z_cci_ord = Z_cci(ord);
%split in the two index parts about conjugate
%center index at order ord
idx_2 = I_2 <= z_cci_ord;
lin_idx_a = sub2ind([N,Z_cci(ord),ord],I_1(idx_2),I_2(idx_2),I_3(idx_2));
pi_dum(I_ord_pos(idx_2)) = data.H{ord}(lin_idx_a);
lin_idx_b = sub2ind([N,Z_cci(ord),ord],I_1(~idx_2),z_ord-I_2(~idx_2)+1,I_3(~idx_2));
pi_dum(I_ord_pos(~idx_2)) = conj(data.H{ord}(lin_idx_b));
run_ord = run_ord +1;
end
The following step multiplies all composition coefficients that correspond to one combination of multi-indices fulfilling condition 1 and 2.
%multiplication
pi_dum = prod(reshape(pi_dum, sz_un(i),[]),1);
Next all the values of
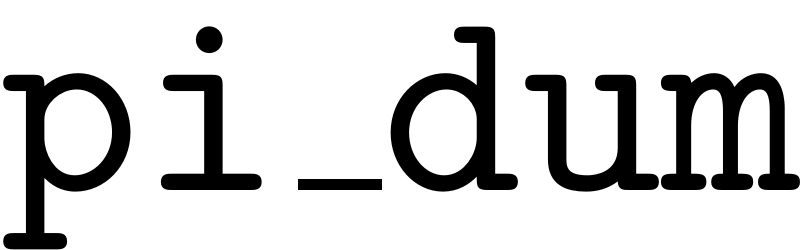 corresponding to the same multi-index
corresponding to the same multi-index
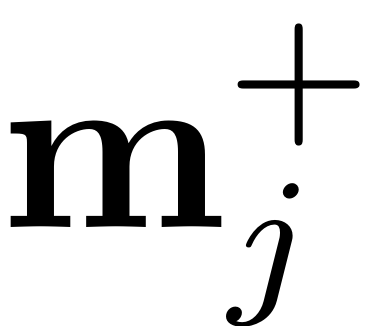 have to be added. This is done by creating an array
have to be added. This is done by creating an array
 that contains for each entry in
that contains for each entry in
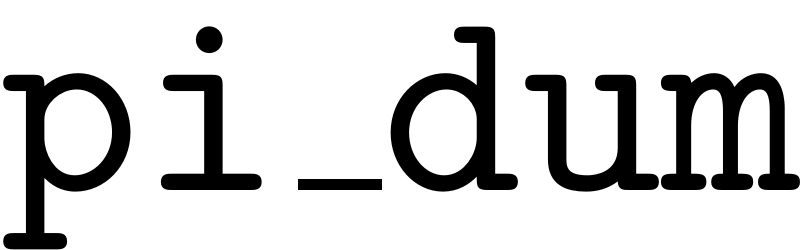 the index
the index
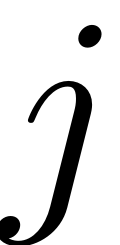 of the size
of the size
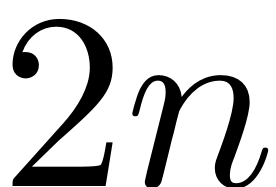 multi-index it corresponds to. Using
multi-index it corresponds to. Using
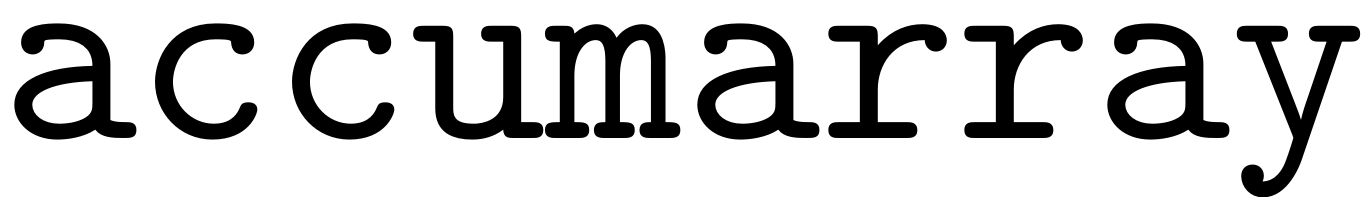 the values that correspond to the same index
the values that correspond to the same index
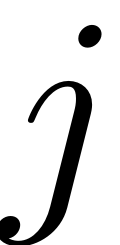 are added up and then stored in the array
are added up and then stored in the array
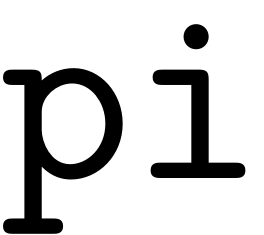 that contains all the composition terms.
that contains all the composition terms.
%sum over combos and put into position list_3 = repelem([1:sumidx].',sum(Cond,1)); % Indices to read out the contributions into correct position n_contrib = sum(Cond,1)>0; idx_pos = find(idx); accum_pi = accumarray(reshape(list_3,[],1),pi_dum); pis(idx_pos(n_contrib),f) = accum_pi(find(n_contrib));
end end
end
