FRC: Level-Set method
Contents
function [FRC] = FRC_level_set(obj, resModes, ORDER, parName, parRange)
FRC level-set method
This function extracts the steady-state amplitude, phase shift and frequency
for periodically forced systems from Forced response curves.
Current implementation assumes forcing of the form
 . For two-dimensional SSMs, we use the normal form of
paramaterization, where we choose the following form of autonomous
reduced dynamics as
. For two-dimensional SSMs, we use the normal form of
paramaterization, where we choose the following form of autonomous
reduced dynamics as
![$$\mathbf{R}_{0}(\mathbf{p})=\left[\begin{array}{c}\lambda p\\\bar{\lambda}\bar{p}\end{array}\right]+\sum_{j=1}^{M}\left[\begin{array}{c}\gamma_{j}p^{j+1}\bar{p}^{j}\\\bar{\gamma}_{j}p^{j}\bar{p}^{j+1}\end{array}\right],$$](FRC_level_set_eq08701743399208904152-Rescaled.png)
and assuming that the
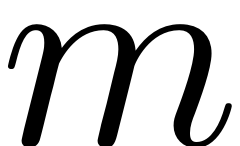 -th harmonic of forcing frequency is nearly resonant with the modal
subspace eigenvalues, i.e.,
-th harmonic of forcing frequency is nearly resonant with the modal
subspace eigenvalues, i.e.,
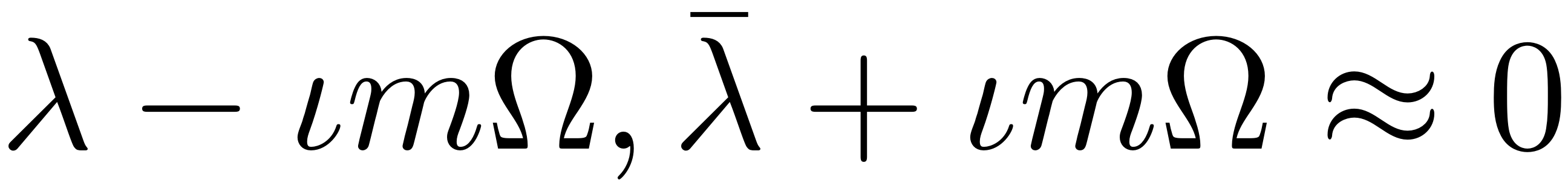 . Denoting
. Denoting
![$\mathbf{W}_{\mathcal{M}}=[\mathbf{w},\,\bar{\mathbf{w}}]\in\mathbf{C}^{N\times2}$](FRC_level_set_eq11559379472127510870-Rescaled.png) , we obtain the leading-order, non-autonomous reduced dynamics using
the normal form parametrization as
, we obtain the leading-order, non-autonomous reduced dynamics using
the normal form parametrization as
![$$\mathbf{R}_{1,0}(\phi)=\left[\begin{array}{c}\mathbf{w}^{\star}\mathbf{F}_{m}^{ext}e^{\iota
m\phi}\\\mathbf{\bar{w}}^{\star}\bar{\mathbf{F}}_{m}^{ext}e^{-\iota m\phi}\end{array}\right],\quad
\dot{\phi}=\Omega$$](FRC_level_set_eq03986938442892099031-Rescaled.png)
We are able to explicitly express the forced response curve as the zero level set of the functions
![$$\mathcal{G}^{\pm}(\rho,\Omega,|f|):=b(\rho,m\Omega)\rho\pm\sqrt{|f|^{2}-\left[a(\rho)\right]^{2}},$$](FRC_level_set_eq01015662870337875341-Rescaled.png)
where
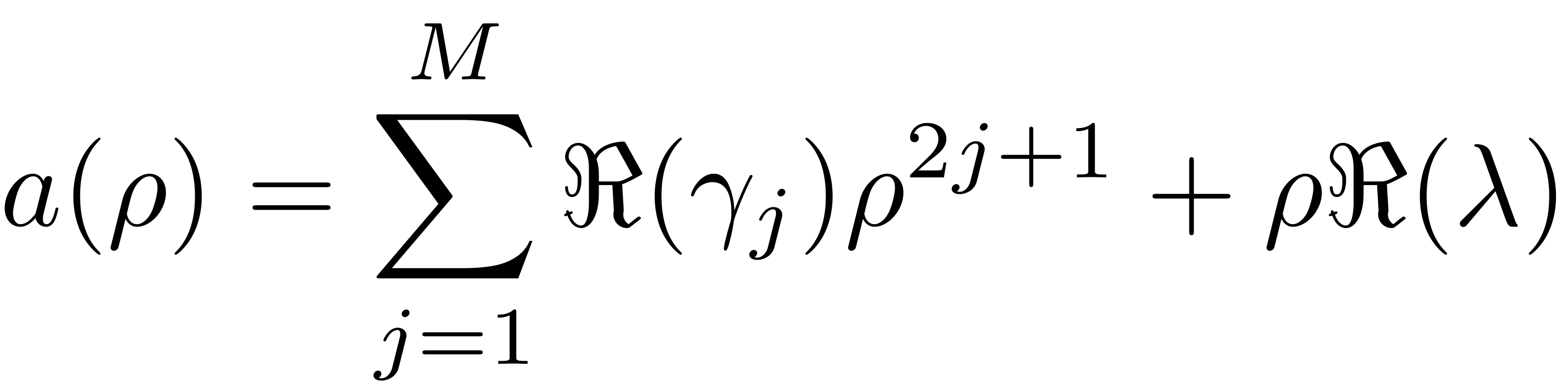
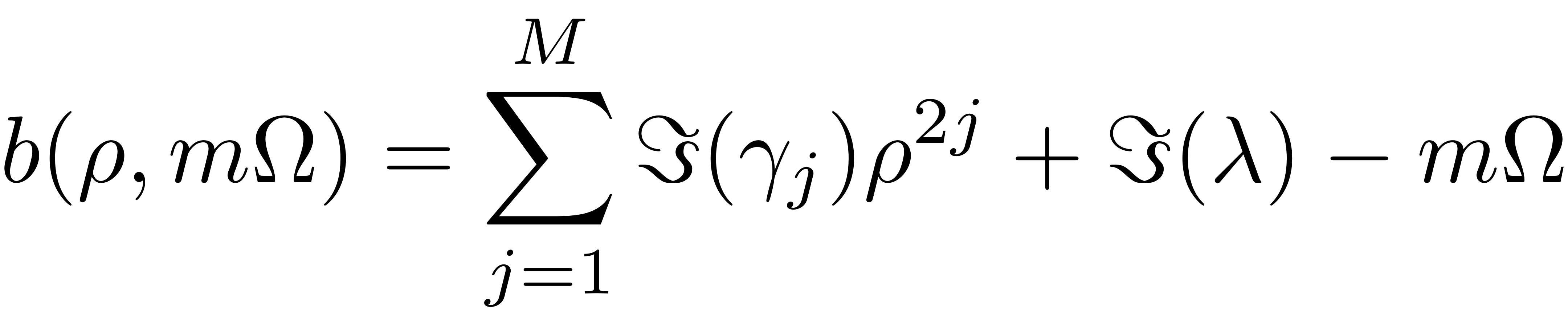
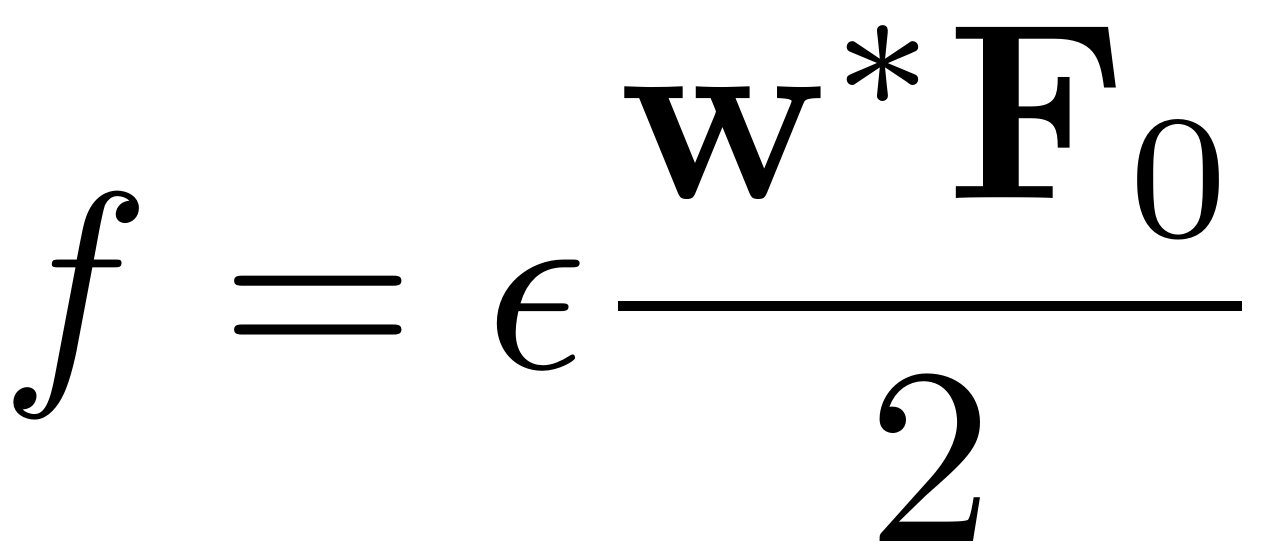
[FRC] = FRC_level_set(obj, resModes, order, parName, parRange)
obj: instance of SSM class
-
resModes: mode pair over which SSM is constructed
-
order: approximation order up until which SSM is computed
-
parName: parameter name in which FRC is constructed
parRange: range of said parameter
FRC: Forced Response Curve data struct
See also: EXTRACT_FRC, FRC_CONTEP, FRC_CONTPO
dimModes = numel(resModes); assert(dimModes==2,'levelset method for FRC extraction is valid only for 2-dimensional SSMs. Please use the continuation method') % compute two dimensional autonomous SSM obj.choose_E(resModes) % highest order ORDER = sort(ORDER); max_order = ORDER(end); num_order = numel(ORDER); AutTic = tic; [W0, R0] = obj.compute_whisker(max_order); obj.FRCInfo.lvlsetTimeAut = toc(AutTic); % autonomous reduced dynamics coefficients gamma = compute_gamma(R0); lambda = obj.E.spectrum(1); % get options [nt, nRho, nPar, rhoScale, nPsi, outdof, saveIC] = ... deal(obj.FRCOptions.nt, obj.FRCOptions.nRho, ... obj.FRCOptions.nPar, obj.FRCOptions.rhoScale, obj.FRCOptions.nPsi,... obj.FRCOptions.outdof, obj.FRCOptions.saveIC); % Initialize FRC as a struct array par = linspace(parRange(1),parRange(end), nPar); FRC = cell(nPar,1);
Grid for evaluation of
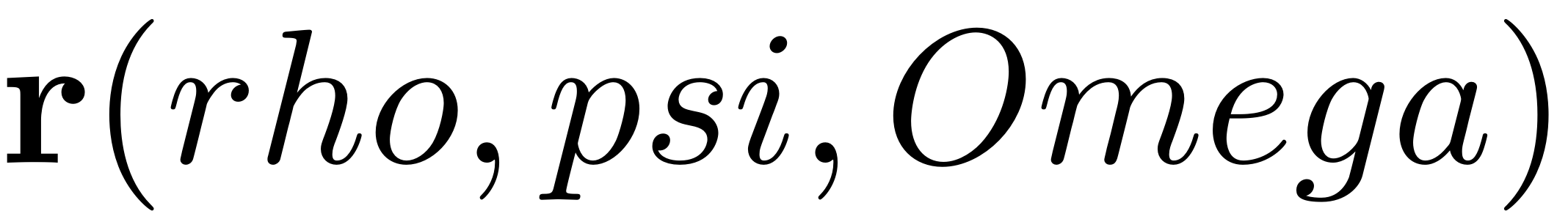
switch lower(parName) case 'freq' % vary Omega keeping epsilon constant Omega_init = par(1); omegaRange = par; epsilon_init = obj.System.Fext.epsilon; case 'amp' % vary epsilon keeping Omega constant Omega_init = obj.System.Omega; omegaRange = Omega_init; epsilon_init = max(parRange); % biggest epsilon for constructing grid end % leading-order modal forcing coefficient f = compute_f(obj,W0,R0,Omega_init); [rho, psi, RHO, PSI] = compute_polar_grid(omegaRange,epsilon_init,gamma,lambda,f,rhoScale, nRho, nPsi);
Obtain FRC
BaseExcitation = obj.System.Options.BaseExcitation; % Check if pool has peen created - user needs to explicitly create pool in % order to use parallel computation of non-autonomous manifold p = gcp('nocreate'); % If no pool, do not create new one. if isempty(p) %|| obj.Options.parallelNL poolsize = 0; else poolsize = p.NumWorkers; end nonAutTic = tic; switch obj.Options.contribNonAuto % ##################################################################### % Computing higher order contributions to W1 and R1 case true parfor (j = 1:nPar,poolsize) Omega = []; % To avoid 'Uninitialized Temporaries' warning epsilon = []; % setup parameters switch lower(parName) case 'freq' % vary Omega keeping epsilon constant Omega = par(j); epsilon = epsilon_init; case 'amp' % vary epsilon keeping Omega constant epsilon = par(j); Omega = Omega_init; end if BaseExcitation epsilon = epsilon*Omega^2; end [W1, R1] = obj.compute_perturbed_whisker(max_order-1,W0,R0,Omega); for order_idx = 1:num_order order = ORDER(order_idx); n_gamma = floor((order-1)/2); [rhodot, rhopsidot, eta] = compute_reduced_dynamics_2D_polar(RHO,PSI, ... lambda, gamma(1:n_gamma), restrict_order(R1,order,'R'),Omega,epsilon); % Numerical computation of fixed points of the reduced dynamics [rho0, psi0] = compute_fixed_points_2D(rho, psi, rhodot, rhopsidot); % Stabilty calculation stability = check_stability(rho0,psi0,gamma(1:n_gamma),lambda,epsilon,restrict_order(R1,order,'R')); % output data structure FRC{j,order_idx} = compute_output_polar2D(rho0,psi0,stability,epsilon,... Omega*ones(size(rho0)),W0(1:order),restrict_order(W1,order,'W'),eta,nt, saveIC, outdof); end end % ##################################################################### % Computing the leading order contribution to R1 case false [~, R1] = obj.compute_perturbed_whisker(0,W0,R0,par(1)); parfor(j = 1:nPar,poolsize) Omega = []; % To avoid 'Uninitialized Temporaries' warning epsilon = []; % setup parameters switch lower(parName) case 'freq' % vary Omega keeping epsilon constant Omega = par(j); epsilon = epsilon_init; case 'amp' % vary epsilon keeping Omega constant epsilon = par(j); Omega = Omega_init; end if BaseExcitation epsilon = epsilon*Omega^2; end for order_idx = 1:num_order order = ORDER(order_idx); n_gamma = floor((order-1)/2); [rhodot, rhopsidot, eta] = compute_reduced_dynamics_2D_polar(RHO,PSI, ... lambda, gamma(1:n_gamma), R1,Omega,epsilon); % Numerical computation of fixed points of the reduced dynamics [rho0, psi0] = compute_fixed_points_2D(rho, psi, rhodot, rhopsidot); % Stabilty calculation stability = check_stability(rho0,psi0,gamma(1:n_gamma),lambda,epsilon,R1); % output data structure FRC{j,order_idx} = compute_output_polar2D(rho0,psi0,stability,epsilon,... Omega*ones(size(rho0)),W0(1:order),[],eta,nt, saveIC, outdof); end end end obj.FRCInfo.lvlsetTimeNonAut = toc(nonAutTic); for j = 1:numel(ORDER) FRCout{j} = cat(1,FRC{:,j}); end
end
function [rho, psi, RHO, PSI] = compute_polar_grid(omegaRange,epsilon,gamma,lambda,f,rhoScale, nRho, nPsi) % *Explicit quadratic approximation of the backbone curve* % % $$\rho_{backbone} = \sqrt{\frac{\Omega-\Im(\lambda)}{\Im(\gamma_1)}}$$ rhomaxBB = max(real(sqrt((omegaRange - imag(lambda))/imag(gamma(1))))); rhomaxlin = full(abs(epsilon * f/real(lambda))); if isempty(f) assert( rhomaxBB ~= 0, 'Estimation of maximal amplitude failed') rhomax = rhoScale * rhomaxBB; else if rhomaxBB ~=0 % heuristically choose maximum value of polar radius as follows rhomax = rhoScale * min(rhomaxBB, rhomaxlin); else rhomax = rhoScale * rhomaxlin; end end %compute grids rho = (rhomax/nRho) * (1:nRho); psi = (2*pi/nPsi) * (0:nPsi-1); [RHO,PSI] = meshgrid(rho,psi); end function [f] = compute_f(obj,W0,R0,Omega) % compute non-autonomous SSM coefficients [~, R1] = obj.compute_perturbed_whisker(0,W0,R0,Omega); f = nonzeros(R1(1).R(1).coeffs); % leading-order modal forcing coefficient end function [Var] = restrict_order(Var,order,type) % restricts paramtersiation or reduced dynamics Var to a certain order nkappas = numel(Var); for kap = 1:nkappas if strcmp(type,'W1') Var(kap).W = Var(kap).W(1:order); elseif strcmp(type,'R1') Var(kap).R = Var(kap).R(1:order); end end end
