EVALUATE_FEXT

function Fext = evaluate_Fext(obj,t,z)

This function evaluates the external forcing at a given time t for a dynamical system object in the first-order form.

The quasiperiodic first order system force is given as a Taylor expansion on coordinates of the physical coordinates:

$\mathbf {F}(\mathbf{z},\mathbf{\phi}) = \left[\begin{array}{c} F^1(\mathbf{z},\mathbf{\phi}) \\ \vdots \\ F^{n}(\mathbf{z},\mathbf{\phi})\end{array}\right], \quad F^i(\mathbf{z},\mathbf{\phi}) = \sum_{\mathbf{n}\in \bf{N}^{n}} F^i_{\mathbf{n}}(\mathbf{\phi}) \mathbf{z}^\mathbf{n}$

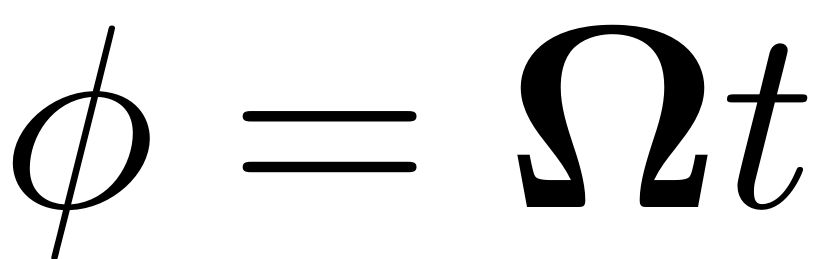
The force coefficients are given as a fourier expansion in terms of the phase variable $\mathbf{\phi} = \mathbf{\Omega}t$

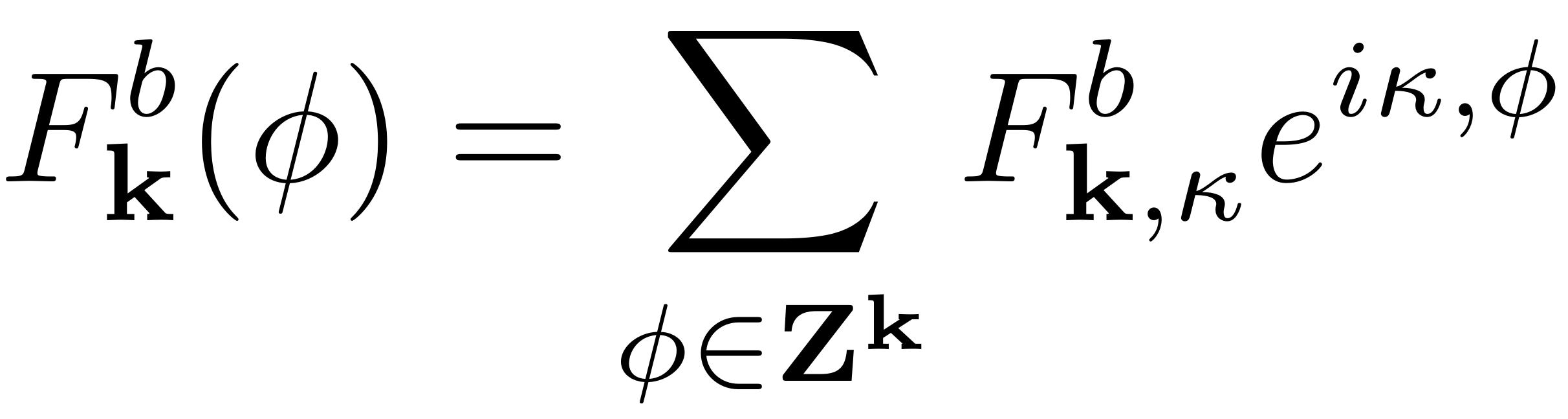
$F^b_{\mathbf{k}}(\mathbf{\phi}) = \sum_{\mathbf{\phi} \in \bf{Z}^k} F^b_{\mathbf{k},\mathbf{\kappa}} e^{i \mathbf{\kappa}, \mathbf{\phi}}$

switch obj.order
    case 1
        if isempty(obj.Fext)
            Fext = sparse(obj.N,1);
        else
            assert(~isempty(obj.Omega), ' Fext cannot be evaluated as the Omega property of the DS class is empty')
            % This function assumes periodic forcing
            nt = size(z,2);
            Fext = zeros(size(obj.N,nt));

            num_kappa = numel(obj.Fext.data);

            for i = 1:num_kappa
                % Highest order this Force contributes at
                order = numel(obj.Fext.data(i).F_n_k)-1;

                % zeroth order
                F0 = obj.Fext.data(i).F_n_k(1);

                if ~isempty(F0) && ~isempty(F0.coeffs)
                    Fext = Fext + real( F0.coeffs * exp(1i *  obj.Fext.data(i).kappa * obj.Omega .* t));
                end

                for j = 1:order % array starting at 0
                    %Contribution to order j Forcing with harmonic kappa_i
                    Fij = obj.Fext.data(i).F_n_k(j+1);
                    Fext = Fext + real(expand_multiindex(Fij,z) .* ...
                        exp(1i *  obj.Fext.data(i).kappa * obj.Omega .* t));
                end
            end
            if obj.order==2
            assert(size(obj.Omega,2) == size(obj.fext.epsilon,2),'epsilon and Omega must have same number of columns');
            else
            assert(size(obj.Omega,2) == size(obj.Fext.epsilon,2),'epsilon and Omega must have same number of columns');
            end
            Fext = Fext * diag(obj.Fext.epsilon);
            if obj.Options.BaseExcitation
                Fext = Fext*diag((obj.Omega).^2);
            end
        end
    case 2
        x  = z(1:obj.n,:);
        xd  = z(obj.n+1:obj.N,:);
        nt = size(x,2);
        Fext = [obj.compute_fext(t,x,xd);
                sparse(obj.n,nt)];
end