An introduction to the computation of Spectral Submanifolds
Contents
First order mechanical systems
We consider dynamical systems of the form
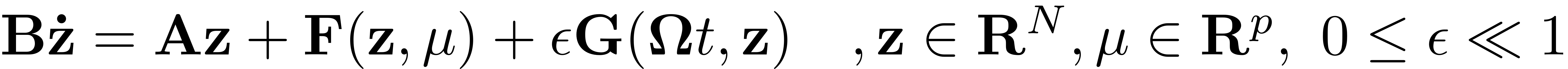
Any first order ODE with smooth right hand side can be brought to
this standard form around its fixed points. After an initial
translation to set a fixed point to the origin of the coordinate
system, the right hand side can be expanded as a Taylor series which
yields the desired form. Here
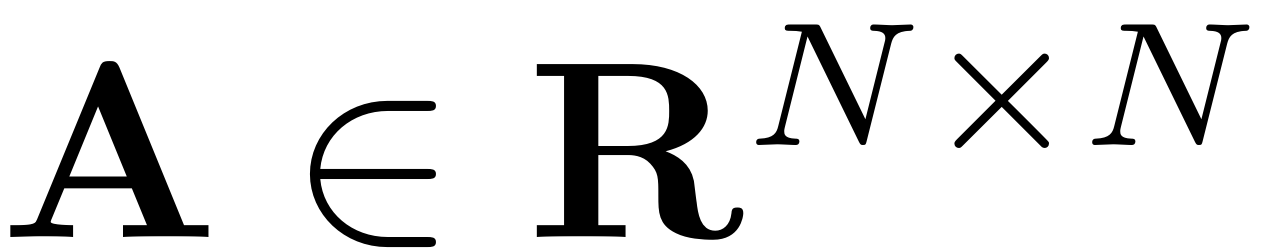 is the linear part of the dynamical system. Throughout the dynamical
systems literature the matrix
is the linear part of the dynamical system. Throughout the dynamical
systems literature the matrix
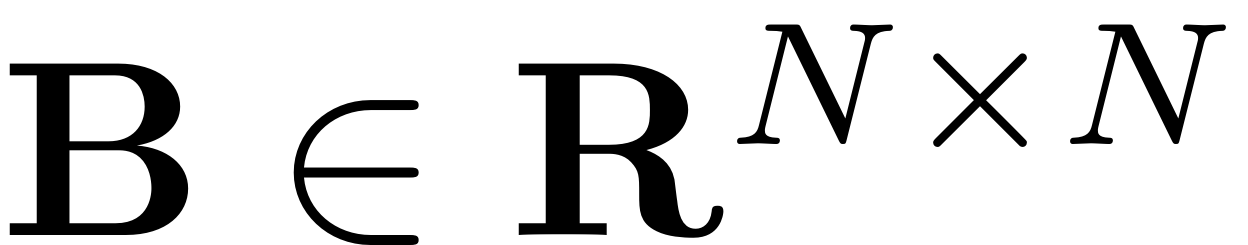 is often taken to be the identity. We do not make this assumption
and treat the general case, which leads to computational advantages
for dynamical systems that stem from second order ODEs as the
inversion of possibly large system matrices can be avoided this way.
is often taken to be the identity. We do not make this assumption
and treat the general case, which leads to computational advantages
for dynamical systems that stem from second order ODEs as the
inversion of possibly large system matrices can be avoided this way.
 is a vector valued nonlinear function and assumed to be
is a vector valued nonlinear function and assumed to be
 -times continuously differentiable in
-times continuously differentiable in
 and a set of parameters
and a set of parameters
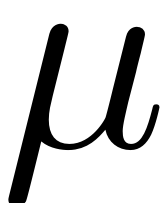 .
.
 is a non-autonomous and possibly non-linear function which contains
the time-dependent forcing that is acting on the system.
is a non-autonomous and possibly non-linear function which contains
the time-dependent forcing that is acting on the system.
Second order mechanical systems
Invariant manifolds such as SSMs can also be computed in the phase space of second order mechanical systems. These look as follows
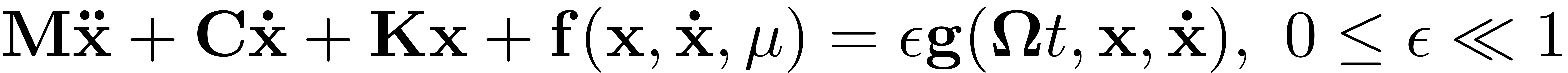
The linear part of the system is characterised by
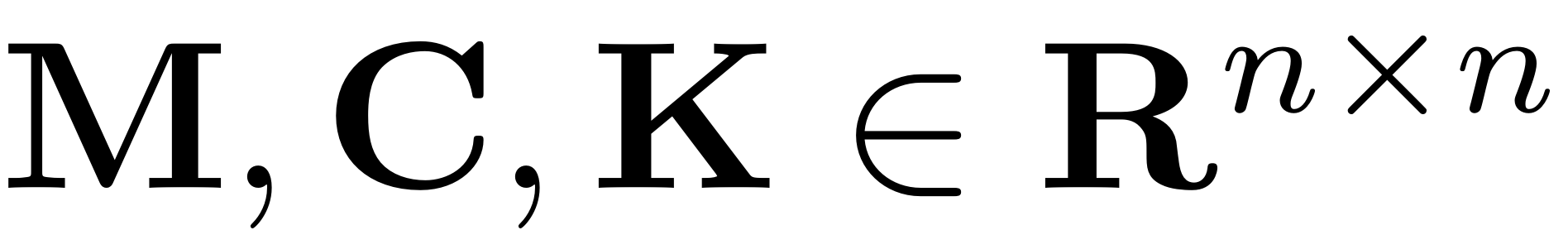 which denote the mass, damping and stiffness matrices, respectively.
The function
which denote the mass, damping and stiffness matrices, respectively.
The function
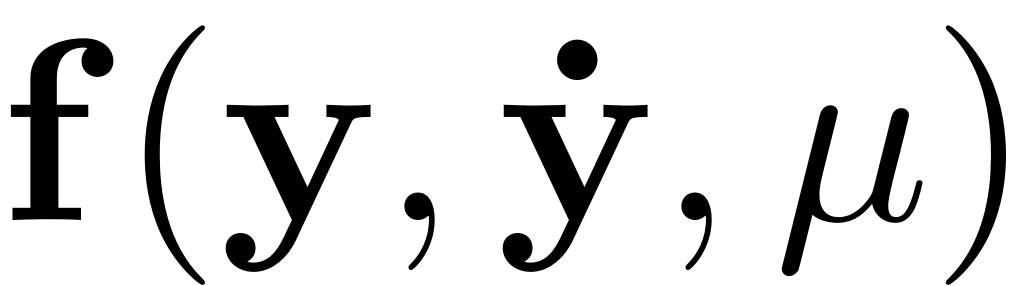 is a nonlinear function that is
is a nonlinear function that is
 times continuously differentiable with
times continuously differentiable with
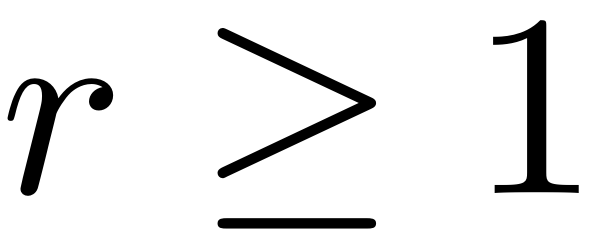 .The distinct types of time-dependent forces are represented by
general forcing vector
.The distinct types of time-dependent forces are represented by
general forcing vector
 . The second order form can be rewritten to the first order form,
for instance by choosing
. The second order form can be rewritten to the first order form,
for instance by choosing
![$$\mathbf{z} = \left[ \begin{array}{c} \mathbf{x} \\ \dot{\mathbf{x}} \end{array}
\right], \quad \mathbf{A} = \left[ \begin{array}{c} -\mathbf{K} \quad \mathbf{0}
\\ \mathbf{0} \quad \mathbf{M} \end{array} \right], \quad \mathbf{B} = \left[ \begin{array}{c}
\mathbf{C} \quad \mathbf{M} \\ \mathbf{M} \quad \mathbf{0} \end{array} \right], \quad
\mathbf{ F(z)} = \left[ \begin{array}{c}- \mathbf{f(x,\dot{x})} \\ \mathbf{0}
\end{array} \right], \quad \mathbf{ G}(\mathbf\Omega t, \mathbf{z}) = \left[
\begin{array} {c} \mathbf{g}(\mathbf\Omega t,\mathbf{x},\mathbf{\dot{x}}) \\
\mathbf{0}\end{array}\right]$$](SSM_Computation_eq06462748947804439120-Rescaled.png)
This choice to obtain the first-order form is not unique (cf. Jain & Haller, 2021) but all such forms can be used for the computation of SSMs. No assumption has to be made about the magnitude of the nonlinearities as the results presented here are valid for nonlinearities of any magnitude, the curvature of the computed manifolds depends smoothly on the magnitude of the nonlinearities.
Parametrisation of SSM and reduced dynamics
To compute the parametrisation of the SSM and the reduced dynamics on it they are expanded as Taylor series. In an initial step, they are expanded in the forcing amplitude, which allows to separate autonomous and non-autonomuos contributions:
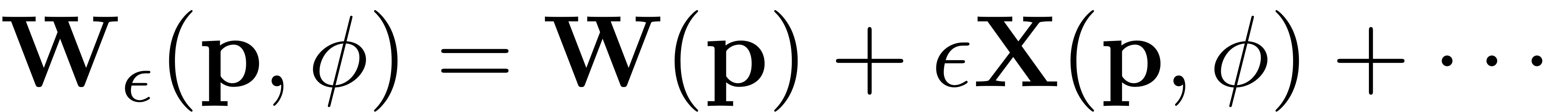
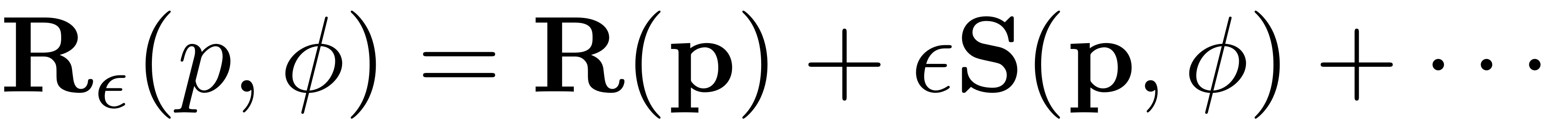
where
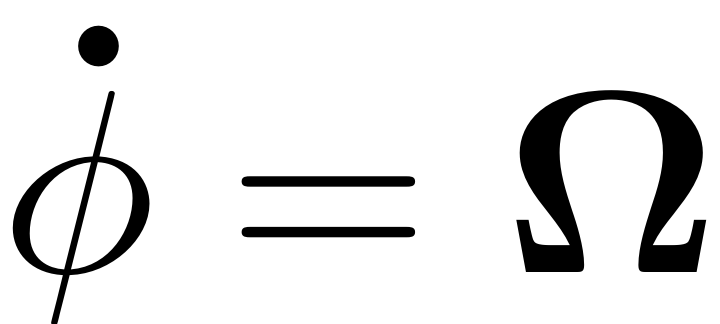 Consequently the individual functions are also expanded in the
parametrisation coordinates
Consequently the individual functions are also expanded in the
parametrisation coordinates
 . For the autonomous functions this reads
. For the autonomous functions this reads


Here we have made use of the multi-index notation, which leads to an
efficient computational routine and easy handling of the terms (cf.
Thurnher, Haller & Jain, 2023). Using a multi-index
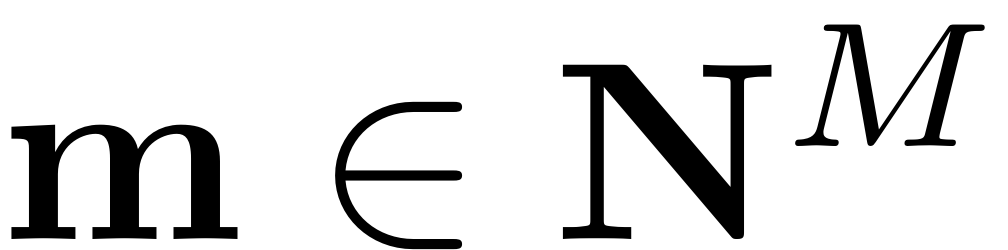 a monomial in parametrisation space can be written in a unique way,
as
a monomial in parametrisation space can be written in a unique way,
as
 . As the non-autonomous parametrisation and reduced dynamics
coefficients depend on time, they are expanded in a Fourier series,
which yields an expression for the non-autonomous functions given in
terms of a Taylor-Fourier expansion:
. As the non-autonomous parametrisation and reduced dynamics
coefficients depend on time, they are expanded in a Fourier series,
which yields an expression for the non-autonomous functions given in
terms of a Taylor-Fourier expansion:
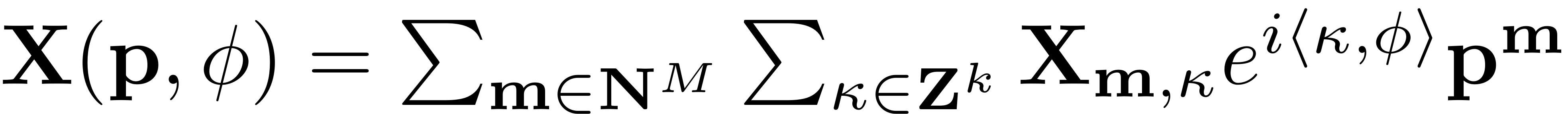
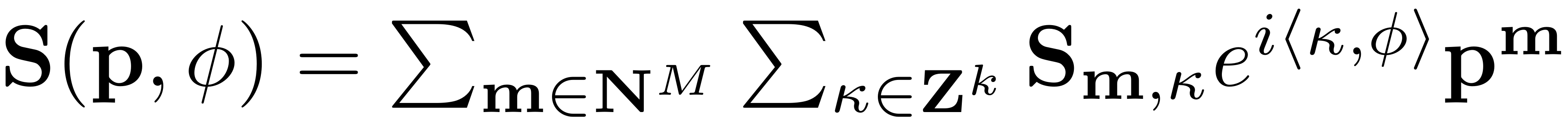
For an account of how the coefficients of the nonlinear functions used in these expansions are used, please refer to the following figure:

Existence and computation of SSMs
In order to check, whether the SSM (we refer to it as
S) that one is about to compute really exists, the
Manifold class automatically performs a resonance
analysis when the modes are chosen with
S.choose_E(masterModes) %automatically performs resonance analysis
Consequently, the information about resonances between the master spectral subspace and the remaining system modes that have been computed, gets stored in the SSM object. If a manifold computation is consequently attempted, the system will prompt information about relevant resonances which might affect the existence of the manifold. More information about this is given in Spectrum and Resonances and Theory of SSMs.
Computation of the autonomous SSM
Now that the existence of the SSM has been established we move to
the computation of the automomous SSM parametrisation
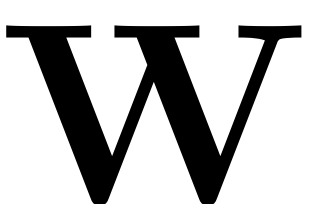 and the reduced dynamics
and the reduced dynamics
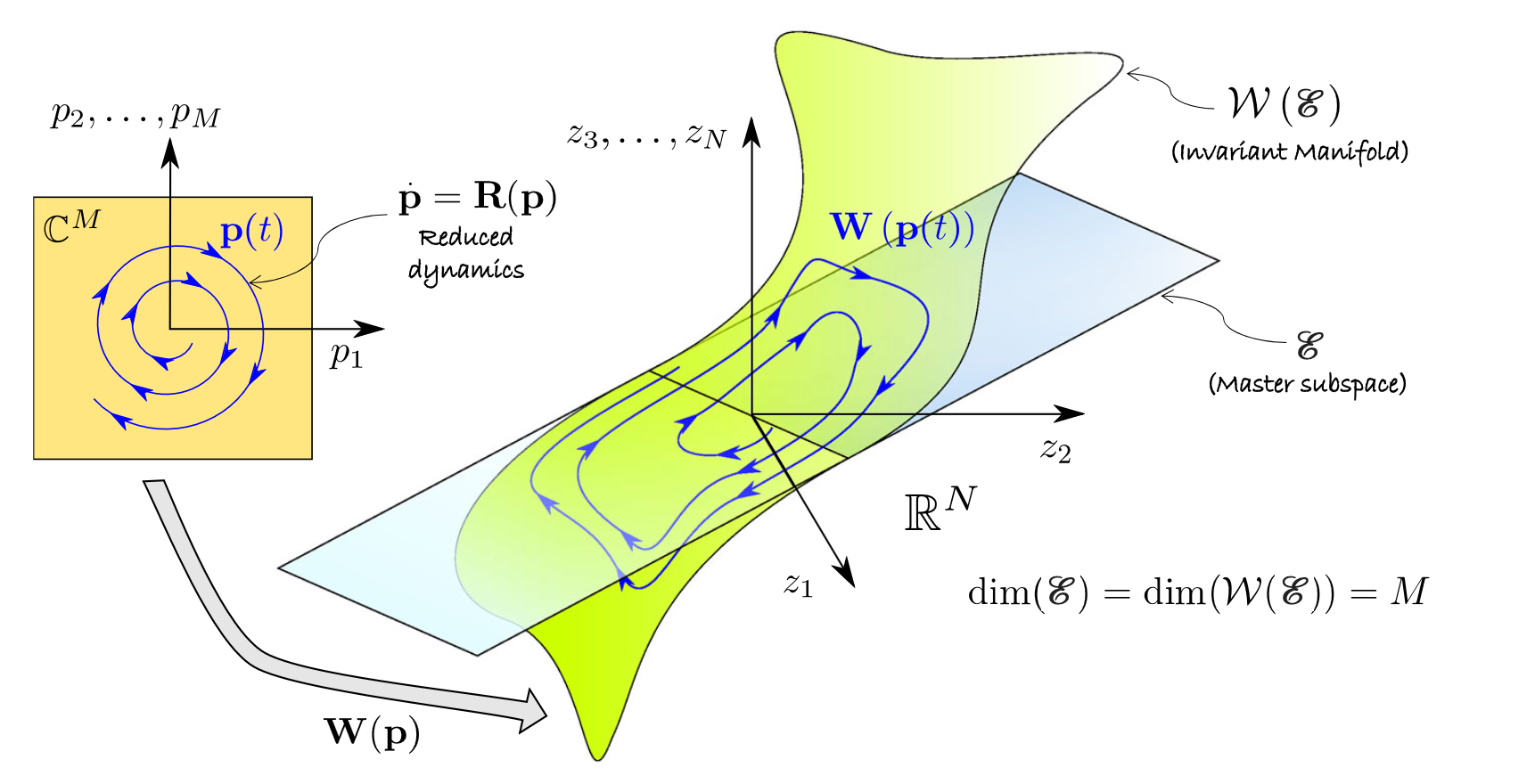
 . The following figure (cf.
Jain & Haller, 2021) depicts, how such an SSM maps the
. The following figure (cf.
Jain & Haller, 2021) depicts, how such an SSM maps the
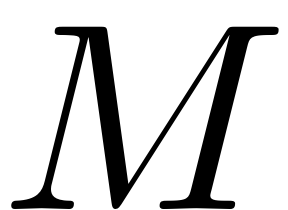 parametrisation coordinates onto a
parametrisation coordinates onto a
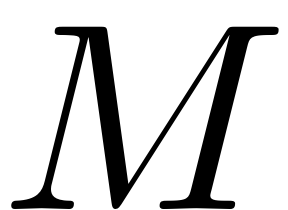 - dimensional manifold
- dimensional manifold
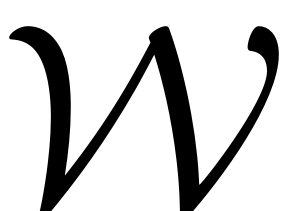 in full phase space. This manifold is tangent to the master spectral
subspace
in full phase space. This manifold is tangent to the master spectral
subspace
 . The reduced dynamics on the SSM are represented by
. The reduced dynamics on the SSM are represented by
 and constitute an exact ROM for the full system. Due to the
invariance, any trajectory of the reduced dynamics in the
parametrisation space is mapped onto a trajectory on
and constitute an exact ROM for the full system. Due to the
invariance, any trajectory of the reduced dynamics in the
parametrisation space is mapped onto a trajectory on
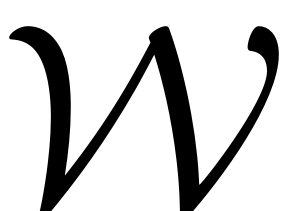 on the full phase space. For an explanation on the underlying theory
of the SSM and the reduced dynamics see
Theory of SSMs. For more explanations
on the choice and importance of
on the full phase space. For an explanation on the underlying theory
of the SSM and the reduced dynamics see
Theory of SSMs. For more explanations
on the choice and importance of
 refer to
Spectrum and Resonances.
refer to
Spectrum and Resonances.
The autonomous contributions to the invariance equation (see SSM-Theory) are collected which yields the autonomous invariance equation
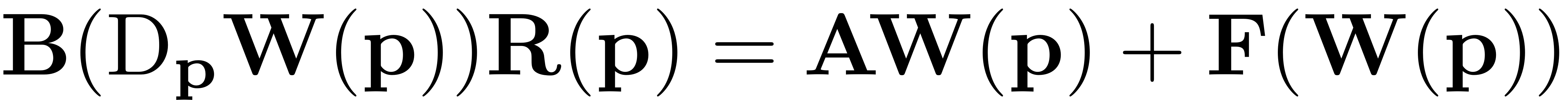
Consequently the expansions for the SSM-parametrisation and the
reduced dynamics are plugged in. As multi-variate monomials are
linearly independent and form a basis in their functional space, the
invariance equation decouples for each multi-index (recall that each
multi-index corresponds to a unique monomial). The cohomological
equation for a multi-index
 reads
reads
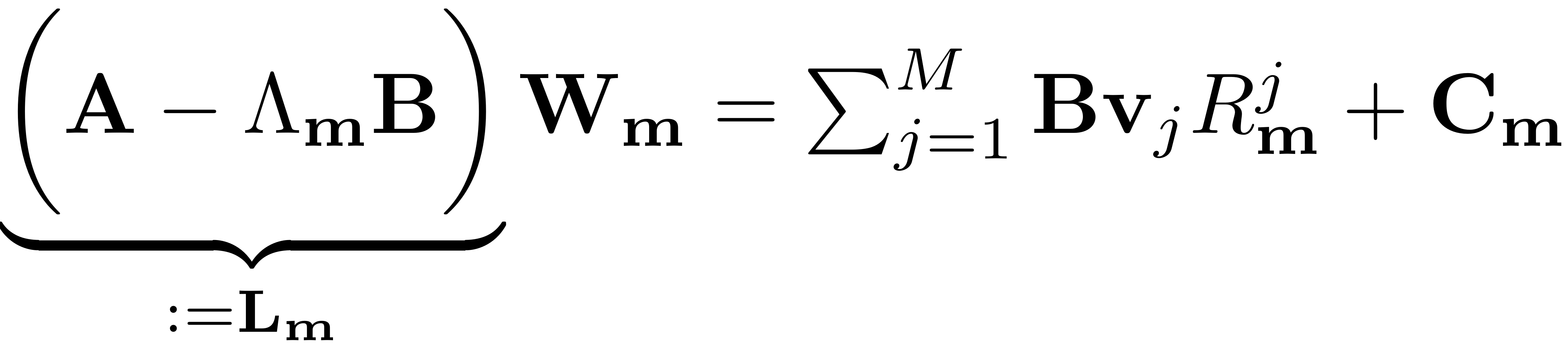
Here we have defined
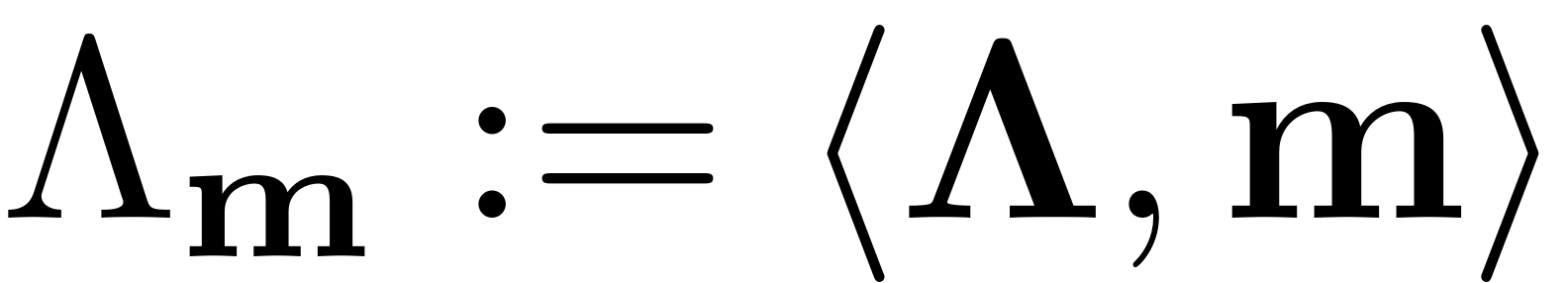 . As this equation is underdetermined (
. As this equation is underdetermined (
 and the number of unknowns is
and the number of unknowns is
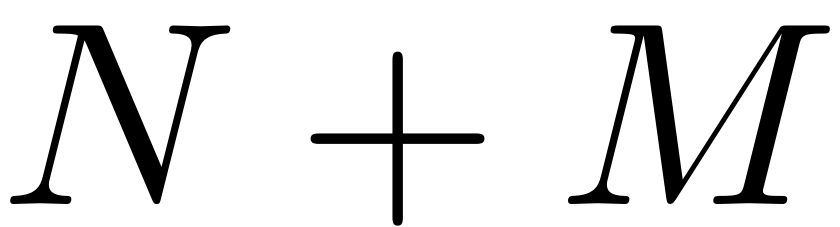 , due to the reduced dynamics coefficients ) we have the freedom to
choose different styles of the parametrisation. For a normal form
parametrisation, the reduced dynamics coefficients are set non-zero
only in the case a resonance occurs. In this case the condition
, due to the reduced dynamics coefficients ) we have the freedom to
choose different styles of the parametrisation. For a normal form
parametrisation, the reduced dynamics coefficients are set non-zero
only in the case a resonance occurs. In this case the condition
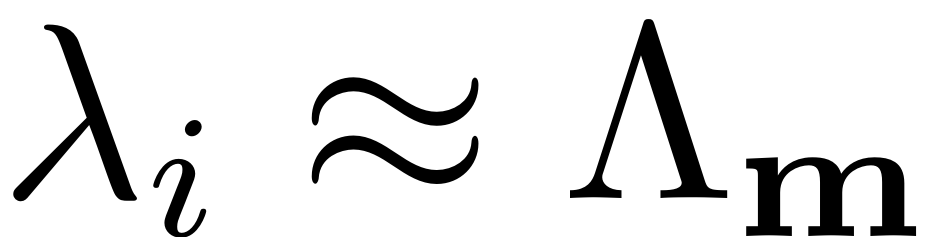
makes the coefficient matrix
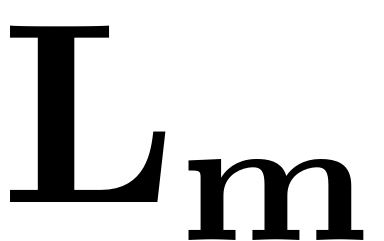 nearly singular. The reduced dynamcis are then chosen to lift this
singularity and render the equation solvable, by choosing
nearly singular. The reduced dynamcis are then chosen to lift this
singularity and render the equation solvable, by choosing
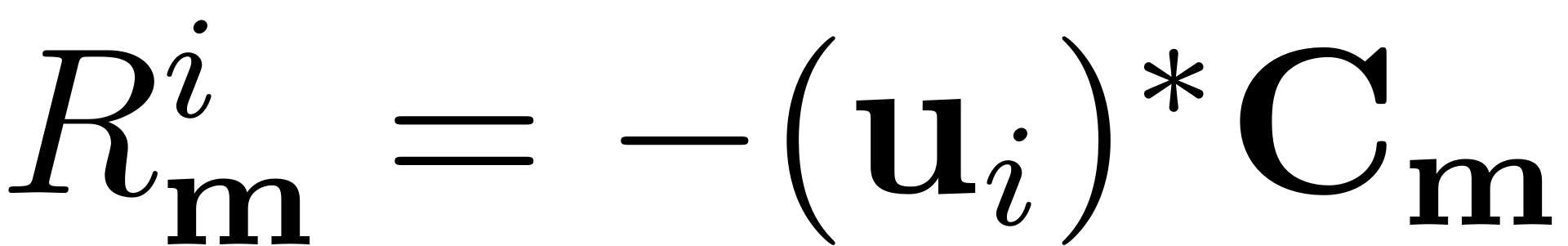
For more details refer to Spectrum and Resonances or to the following publications: Jain & Haller, 2021. and Thurnher, Haller & Jain, 2023.
To compute an approximation to the SSM with SSMTool up to order
order one can simply call
[W,R]=S.compute_whisker(order);
which automatically solves the cohomological equations up to a desired order.
Computation of the non-autonomous SSM
In the case of a non-autonomous dynamical system, the computation of
the non-autonomous parametrisation
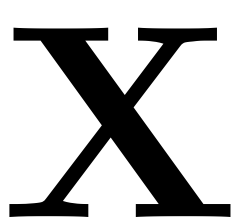 and the non-autonomous contributions of the reduced dynamics
and the non-autonomous contributions of the reduced dynamics
 may be necessary. The non-autonomous, order
may be necessary. The non-autonomous, order
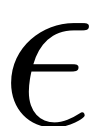 contribution to the invariance equation reads
contribution to the invariance equation reads
![$$\mathbf{B} \bigg( (\textrm{D}_{\mathbf p} \mathbf{W} )\mathbf{S} +
(\partial_{\mathbf p} \mathbf{X} ) \mathbf{R} + (\partial_{\mathbf\phi} \mathbf{X
}) \mathbf\Omega \bigg) = \mathbf{A}\mathbf{X} + \big[\textrm{D}_{\mathbf
z}\mathbf{F} \circ \mathbf{W} \big]\mathbf{X} + \mathbf{G} \circ \mathbf{W}$$](SSM_Computation_eq05281073062084194338-Rescaled.png)
The leading order terms in
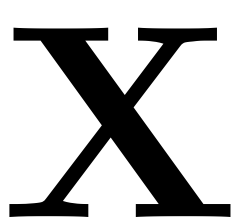 lead to an oscillation of the base to which the autonomous manifold
is attached, while higher order terms account for the (quasi-)
periodic deformation of the manifold itself. Note, that the
non-autonomous effects are of magnitude
lead to an oscillation of the base to which the autonomous manifold
is attached, while higher order terms account for the (quasi-)
periodic deformation of the manifold itself. Note, that the
non-autonomous effects are of magnitude
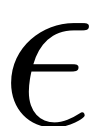 and thus in many cases (in particular if only direct external
excitation resonant to a single mode is present) this term can be
neglected.
and thus in many cases (in particular if only direct external
excitation resonant to a single mode is present) this term can be
neglected.
Leading order approximation
In such a case only a leading order approximation of the non-autonomous reduced dynamics is computed. The higher order non-autonomous terms of the manifold are ignored. The following parameter may be set, to omit higher order non-autonomous terms.
set(S.Options,'contribNonAuto',false)
As the ROM and SSM-coefficients are then independent of the forcing frequency, the invariance equation only has to be solved once - this leads to a fast computational routine. The leading order invariance equation is given as
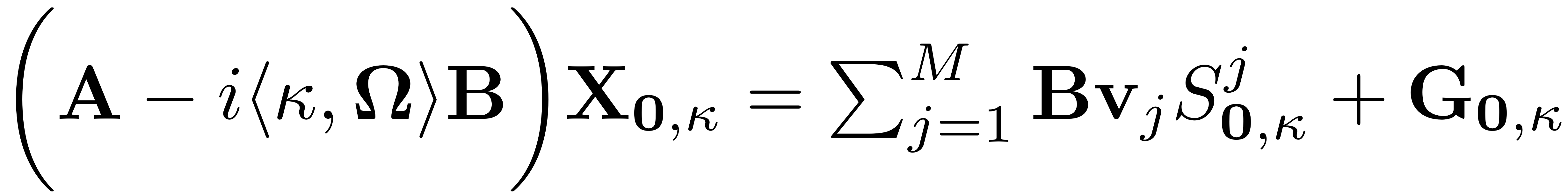
The ROM now reads
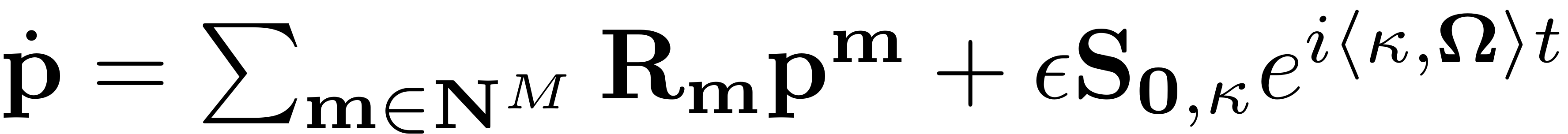
where the non-autonomous coefficient has been chosen as
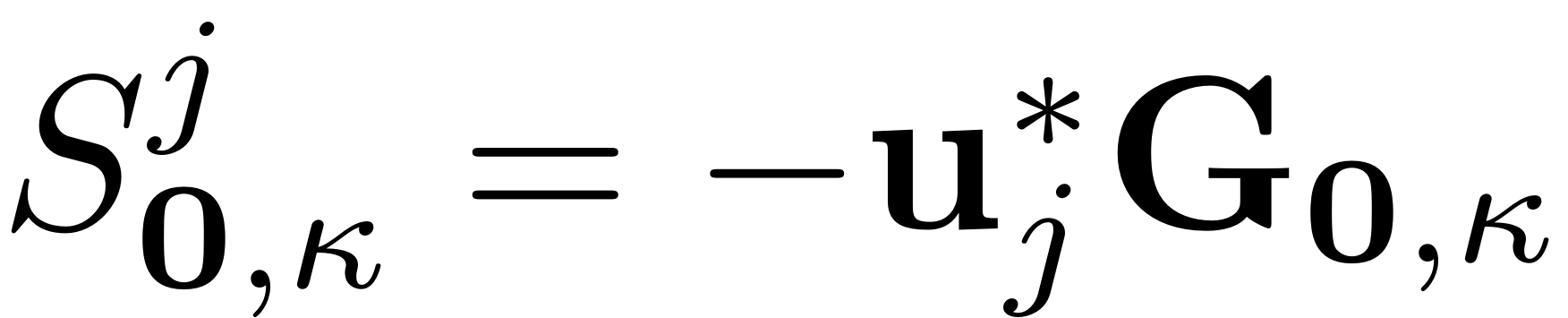 (note that the normalisation of the linear modes is
(note that the normalisation of the linear modes is
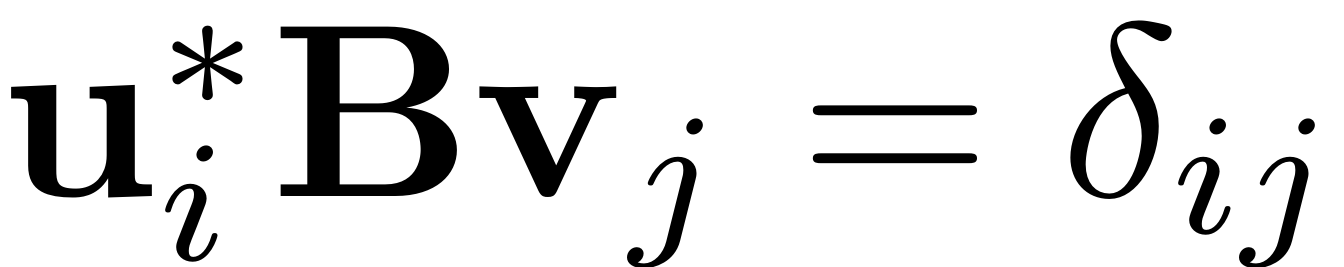 ) to lift the direct resonance
) to lift the direct resonance

Higher order approximation
If more complex resonances or physical effects such as parametric excitation, subharmonic resonances or a more accurate computation is desired, then the non-autonomous terms have to be added to the expansion. Higher order terms of the expansion are included by setting
set(S.Options,'contribNonAuto',true)
The non-autonomous invariance equation for higher order terms reads
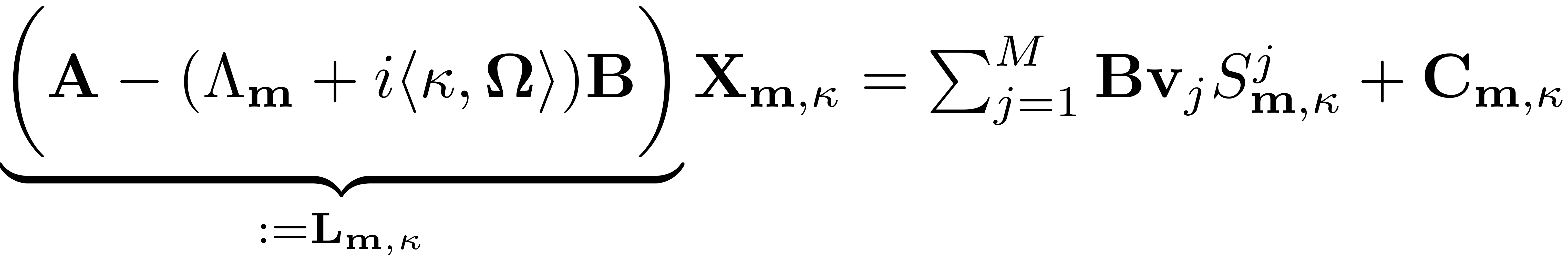
Again,
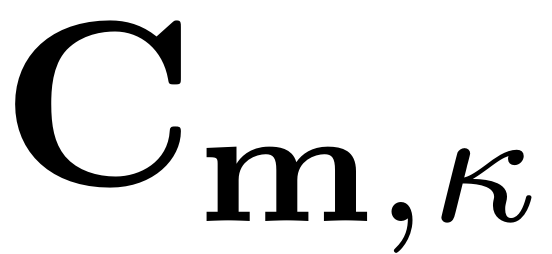 collects known terms corresponding to lower order expansions, the
nonlinear internal forces and the time-dependent forces. The reduced
dynamics are chosen to lift the singularity due to resonances of the
form
collects known terms corresponding to lower order expansions, the
nonlinear internal forces and the time-dependent forces. The reduced
dynamics are chosen to lift the singularity due to resonances of the
form
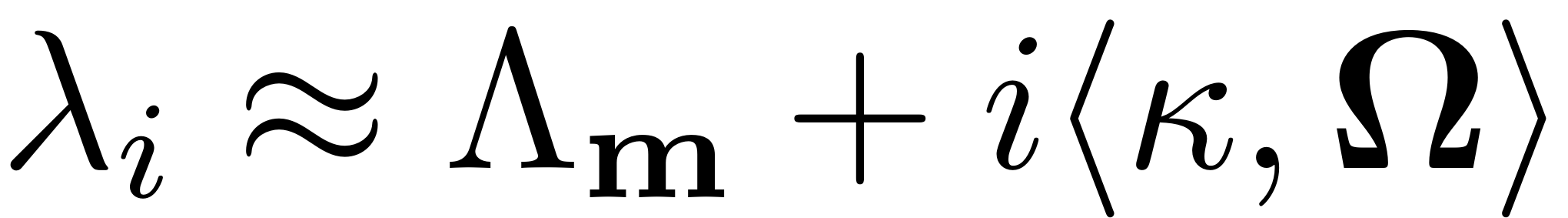
and are set as
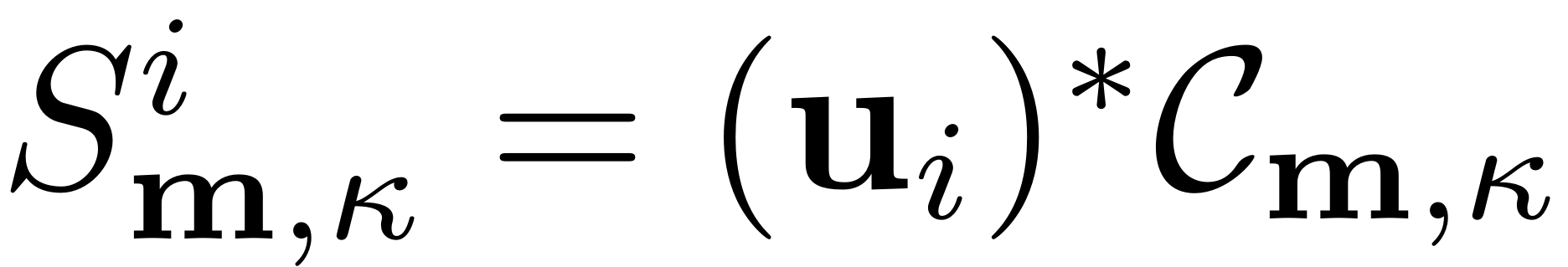
Details on the computational procedure are given in Thurnher, Haller & Jain, 2023. The non-autonomous terms can be computed by calling
S.compute_perturbed_whisker(order,W0,R0,Omega)
Note that for this, W0 and R0 need to be
provided up to order+1, due to the structure of the
non-autonomous equations, and the forcing frequency corresponds to
the frequency at which the non-autonomous terms should be computed.
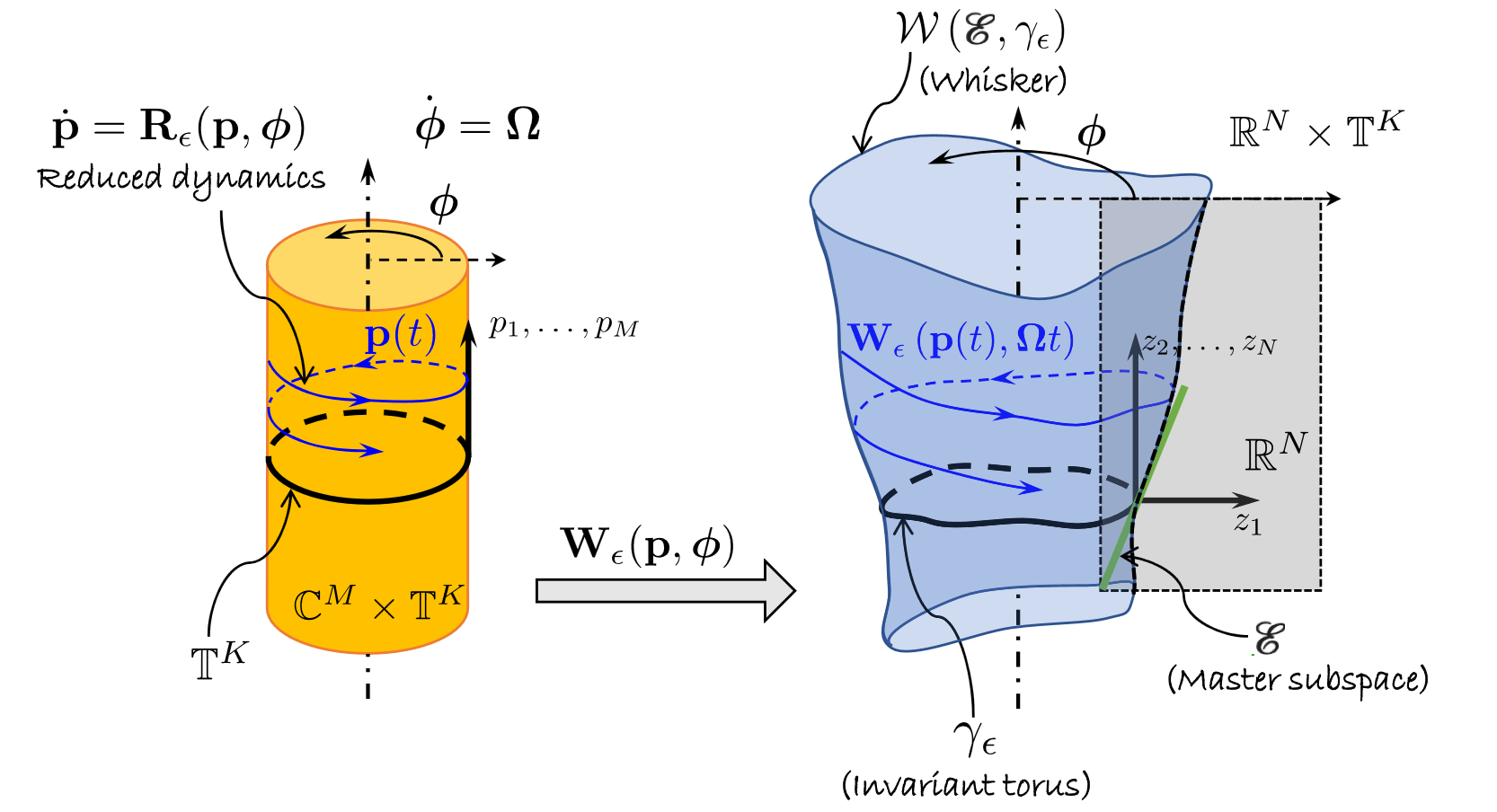
In the following figure (cf.
Jain & Haller, 2021), the parametrisation of such a non-autonomous SSM and the reduced
dynamics on it are visualised schematically. The parametrisation
space (yellow) consists of a direct product of
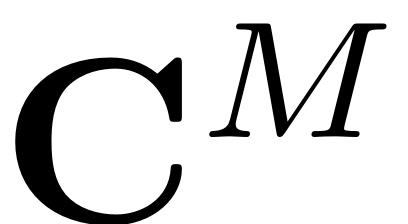 , which contains the spacial parametrisation coordinates, with the
, which contains the spacial parametrisation coordinates, with the
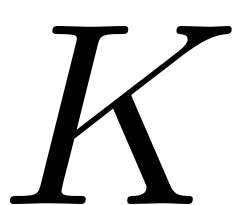 - dimensional torus
- dimensional torus
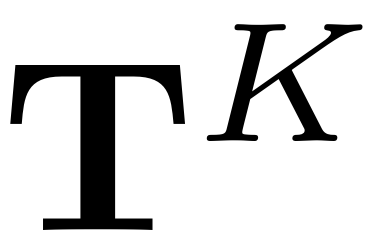 , which includes the temporal variables. The parametrisation
, which includes the temporal variables. The parametrisation
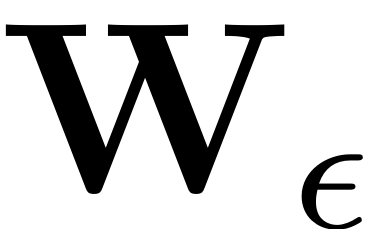 then maps this direct product onto the invariant, non-autonomous
manifold (blue) in the full, non-autonomous phase space. The spatial
euclidian coordinates of this phase space are represented with a
gray rectangle. The master subspace
then maps this direct product onto the invariant, non-autonomous
manifold (blue) in the full, non-autonomous phase space. The spatial
euclidian coordinates of this phase space are represented with a
gray rectangle. The master subspace
 is displayed in green. The temporal evolution of the manifold
parametrisation implies that, as time passes, the SSM stays tangent
to the subbundle
is displayed in green. The temporal evolution of the manifold
parametrisation implies that, as time passes, the SSM stays tangent
to the subbundle
 . The SSM furthermore deformes in a quasiperiodic manner, according
to the frequencies and harmonics present in the external excitation.
. The SSM furthermore deformes in a quasiperiodic manner, according
to the frequencies and harmonics present in the external excitation.