Autonomous reduced dynamics

function y = auto_red_dyn(p, data)

This function presents a vectorized implementation of vector field of reduced dynamics of autonomous SSMs, namely, 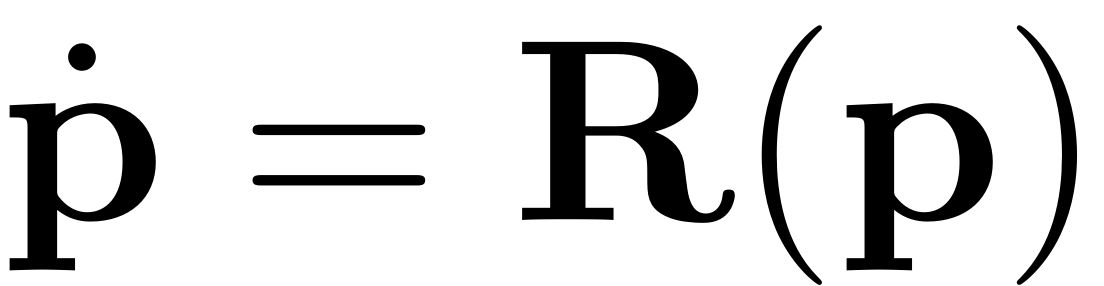$\dot{\bf{p}}=\bf{R(p)}$ . The p vector here is a mixture of both real and complex-conjugate pair variables, the parametrisation variables.

assert(~isempty(data), 'Structure data is empty');
% extract data fields
lamd  = data.lamd;
beta  = data.beta;
kappa = data.kappa;

y = lamd.*z;

% nonlinear part
nTerms = size(kappa,1);
for i=1:nTerms
   coeffs = beta(:,i);
   if max(abs(coeffs))>1e-8
       terms  = z_power_ka(z, kappa(i,:));
       y = y+coeffs*terms;
   end
end

end


function y = z_power_ka(z, ka)
% Z_POWER_KA This function computes complex monomilal z^ka, where
% z=[z1,...,zm] and ka=[ka1,...,kam] and z^ka=z1^ka1*...*zm^kam. Here we
% support vectorized version of z^ka. Specifically, z could be a m-by-n
% matrix, where each row corresponds the component sampled at different
% locations. However, we assume ka to be a vector

m = size(z,1);
% assert(m==numel(ka), 'The dimension of z and ka is not matched');

y = 1;
for i=1:m
    y = y.*z(i,:).^ka(i);
end

end