Oscillatory system with 2:1 internal resonance

Consider the following system with 2 dofs

$\ddot{x}_1+c_1\dot{x}_1+x_1+b_1x_1x_2=\epsilon f_1\cos\Omega t$

$\ddot{x}_2+c_2\dot{x}_2+4x_2+b_2x_1^2=\epsilon f_2\cos\Omega t$

It follows that the system has 1:2 internal resonance. Given damping coefficients $c_{1,2}$ , nonlinear spring coefficients $b_{1,2}$ and forcing coefficients $f_{1,2}$ , the solution manifold of such system is of two dimension and can be parameterized by $(\epsilon,\Omega)$ in general. We use this example to demonstrate

SSM_isol2ep: continuation of equilibrium points in slow-phase normal-form dynamics (corresponding to periodic orbits in the original system) in either forcing frequency $\Omega$ or forcing amplitude $\epsilon$ . The continuation here starts from an initial solution (isol);
SSM_ep2ep: continuation of equilibrium points in slow-phase reduced dynamics (corresponding to periodic orbits in the original system) in either forcing frequency $\Omega$ or forcing amplitude $\epsilon$ . The continuation here starts from a saved solution to equilibrium points (ep);
SSM_ep2SN: continuation of saddle-node (SN) bifurcation equilibrium points in slow-phase normal-form dynamics (corresponding to SN bifurcation periodic orbits in the original system) in $(\Omega,\epsilon)$ . The continuation here starts from a saved ep solution, which is also a SN equilibrium point;
SSM_ep2HB: continuation of Hopf bifurcation (HB) equilibrium points in slow-phase normal-form dynamics (corresponding to Neimark-Sacker or torus (TR) bifurcation periodic orbits in the original system) in $(\Omega,\epsilon)$ . The continuation here starts from a saved ep solution, which is also a HB equilibrium point;
SSM_BP2ep: continuation of equilibrium points in slow-phase normal-form dynamics. The continuation here starts from a saved branch point (BP) solution, which is also an ep equilibrium point;

clear all

Setup model

m = 1;
c1 = 5e-3;
c2 = 1e-2;
b1 = 1;
b2 = 1;
f1 = 1;
f2 = 0;
[mass,damp,stiff,fnl,fext] = build_model(c1,c2,b1,b2,f1,f2);


order = 2;
DS = DynamicalSystem(order);
set(DS,'M',mass,'C',damp,'K',stiff,'fnl',fnl);
set(DS.Options,'Emax',5,'Nmax',10,'notation','multiindex')

Set up the forcing

epsilon = 1e-2;
kappas  = [-1; 1];
coeffs  = [fext fext]/2;
DS.add_forcing(coeffs, kappas, epsilon);

Perform Linear Modal Analysis

[V,D,W] = DS.linear_spectral_analysis();

 The first 4 nonzero eigenvalues are given as 
  -0.0025 + 1.0000i
  -0.0025 - 1.0000i
  -0.0050 + 2.0000i
  -0.0050 - 2.0000i

SSM computation

S = SSM(DS);
set(S.Options, 'reltol', 1,'notation','multiindex');
resonant_modes = [1 2 3 4]; % choose master spectral subspace
mFreq  = [1 2];              % internal resonance relation vector
order  = 3;                  % SSM expansion order
outdof = [1 2 3];           % outdof for output

SSM_epSweeps:

continuation of FRC w.r.t $\Omega$ at sampled $\{\epsilon_i\}$ Before diving into the list of functions mentioned above, we demonstrate SSM_epSweeps, a function built based on the SSM_isol2ep and SSM_ep2ep. It

continues in $\epsilon$ (with fixed $\Omega$ ) and labels the solutions that satisfies $\epsilon=\epsilon_i$ with UZ,
continues in $\Omega$ (with $\epsilon\equiv\epsilon_i$ ) for each $\epsilon_i$ ,
plots FRCs

set(S.FRCOptions,'sampStyle', 'cocoBD');                         % sampling style
set(S.contOptions, 'PtMX', 200, 'ItMX', 15, 'h_max', 0.1,'h_min',0.01);    % continuation setting
set(S.FRCOptions, 'nCycle',5000, 'initialSolver', 'fsolve');     % initial solution scheme
set(S.FRCOptions, 'coordinates', 'polar');                       % two coordinate representations

epsSamp = [0.001 0.003 0.005 0.007 0.01]
freqRange = [0.7 1.1]*imag(D(1));
S.SSM_epSweeps('sweeps',resonant_modes,order,mFreq,epsSamp,freqRange,outdof);

epsSamp =

    0.0010    0.0030    0.0050    0.0070    0.0100

The master subspace contains the following eigenvalues
 
lambda1 == - 0.0025 + 1i
 
lambda2 == (-0.0025) - 1i
 
lambda3 == - 0.005 + 2i
 
lambda4 == (-0.005) - 2i
 
sigma_out = 0
sigma_in = 1
Manifold computation time at order 2 = 00:00:04
Estimated memory usage at order  2 = 1.25E-02 MB
Manifold computation time at order 3 = 00:00:00
Estimated memory usage at order  3 = 2.04E-02 MB

Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the value of the function tolerance, and
the problem appears regular as measured by the gradient.


 Run='sweepseps.ep': Continue equilibria with varied epsilon.

    STEP   DAMPING               NORMS              COMPUTATION TIMES
  IT SIT     GAMMA     ||d||     ||f||     ||U||   F(x)  DF(x)  SOLVE
   0                          6.81e-10  9.93e+00    0.0    0.0    0.0

 STEP      TIME        ||U||  LABEL  TYPE           eps         rho1         rho2          th1          th2           om
    0  00:00:00   9.9315e+00      1  EP      1.0000e-02   6.4627e-02   2.8042e-01   3.9131e+00   5.7812e+00   1.0000e+00
    1  00:00:00   9.9315e+00      2  UZ      1.0000e-02   6.4627e-02   2.8042e-01   3.9131e+00   5.7812e+00   1.0000e+00
    1  00:00:00   9.9332e+00      3  UZ      7.0000e-03   5.7140e-02   2.1921e-01   3.9138e+00   5.7849e+00   1.0000e+00
    2  00:00:01   9.9351e+00      4  UZ      5.0000e-03   5.0820e-02   1.7340e-01   3.9144e+00   5.7878e+00   1.0000e+00
    3  00:00:01   9.9384e+00      5  UZ      3.0000e-03   4.2426e-02   1.2085e-01   3.9152e+00   5.7914e+00   1.0000e+00
    4  00:00:01   9.9456e+00      6  UZ      1.0000e-03   2.8284e-02   5.3709e-02   3.9170e+00   5.7975e+00   1.0000e+00
    4  00:00:01   9.9464e+00      7  EP      9.0000e-04   2.7155e-02   4.9507e-02   3.9172e+00   5.7981e+00   1.0000e+00

 STEP      TIME        ||U||  LABEL  TYPE           eps         rho1         rho2          th1          th2           om
    0  00:00:01   9.9315e+00      8  EP      1.0000e-02   6.4627e-02   2.8042e-01   3.9131e+00   5.7812e+00   1.0000e+00
    1  00:00:01   9.9311e+00      9  EP      1.1000e-02   6.6778e-02   2.9940e-01   3.9128e+00   5.7801e+00   1.0000e+00

 Run='sweepseps1.ep': Continue equilibria with varied omega at eps equal to 1.000000e-03.

    STEP   DAMPING               NORMS              COMPUTATION TIMES
  IT SIT     GAMMA     ||d||     ||f||     ||U||   F(x)  DF(x)  SOLVE
   0                          2.36e-14  1.00e+01    0.0    0.0    0.0

 STEP      TIME        ||U||  LABEL  TYPE            om         rho1         rho2          th1          th2          eps
    0  00:00:00   9.9958e+00      1  EP      1.0000e+00   2.8284e-02   5.3709e-02   3.9170e+00   5.7975e+00   1.0000e-03
    6  00:00:00   9.5734e+00      2  HB      9.9801e-01   3.1756e-02   5.3118e-02   3.5279e+00   5.6902e+00   1.0000e-03
   10  00:00:00   9.5115e+00      3          9.9692e-01   3.5391e-02   5.3158e-02   3.4247e+00   5.7015e+00   1.0000e-03
   20  00:00:00   9.5462e+00      4          9.9576e-01   3.9678e-02   5.3817e-02   3.3781e+00   5.7583e+00   1.0000e-03
   30  00:00:01   9.9391e+00      5          9.9263e-01   5.1821e-02   5.8028e-02   3.4238e+00   6.0563e+00   1.0000e-03
   40  00:00:01   1.0922e+01      6          9.8861e-01   6.7265e-02   6.5321e-02   3.6946e+00   6.7089e+00   1.0000e-03
   50  00:00:01   1.1913e+01      7          9.8656e-01   7.3726e-02   6.6904e-02   3.9978e+00   7.3477e+00   1.0000e-03
   60  00:00:02   1.2832e+01      8  FP      9.8600e-01   7.2692e-02   6.2507e-02   4.2879e+00   7.9351e+00   1.0000e-03
   60  00:00:02   1.2832e+01      9  SN      9.8600e-01   7.2692e-02   6.2507e-02   4.2879e+00   7.9351e+00   1.0000e-03
   60  00:00:02   1.2905e+01     10          9.8600e-01   7.2338e-02   6.1913e-02   4.3112e+00   7.9815e+00   1.0000e-03
   70  00:00:02   1.3899e+01     11          9.8657e-01   6.3922e-02   5.0324e-02   4.6303e+00   8.6124e+00   1.0000e-03
   80  00:00:02   1.4894e+01     12          9.8757e-01   4.9605e-02   3.2625e-02   4.9520e+00   9.2416e+00   1.0000e-03
   84  00:00:03   1.5231e+01     13  SN      9.8772e-01   4.3504e-02   2.5373e-02   5.0603e+00   9.4559e+00   1.0000e-03
   84  00:00:03   1.5231e+01     14  FP      9.8772e-01   4.3504e-02   2.5372e-02   5.0603e+00   9.4559e+00   1.0000e-03
   90  00:00:03   1.5887e+01     15          9.8624e-01   2.9260e-02   1.0282e-02   5.2603e+00   9.8771e+00   1.0000e-03
  100  00:00:03   1.6691e+01     16          9.3233e-01   5.2227e-03   6.7614e-05   5.4608e+00   1.0421e+01   1.0000e-03
  110  00:00:04   1.6778e+01     17          8.2837e-01   2.0598e-03   4.1489e-06   5.4832e+00   1.0488e+01   1.0000e-03
  115  00:00:04   1.6794e+01     18  EP      7.0000e-01   1.1785e-03   7.7699e-07   5.4895e+00   1.0507e+01   1.0000e-03

 STEP      TIME        ||U||  LABEL  TYPE            om         rho1         rho2          th1          th2          eps
    0  00:00:04   9.9958e+00     19  EP      1.0000e+00   2.8284e-02   5.3709e-02   3.9170e+00   5.7975e+00   1.0000e-03
    6  00:00:05   1.0394e+01     20  HB      1.0018e+00   3.1304e-02   5.3569e-02   4.2741e+00   5.8943e+00   1.0000e-03
   10  00:00:05   1.0474e+01     21          1.0029e+00   3.5081e-02   5.3809e-02   4.3885e+00   5.8809e+00   1.0000e-03
   20  00:00:05   1.0445e+01     22          1.0040e+00   3.9174e-02   5.4625e-02   4.4335e+00   5.8206e+00   1.0000e-03
   30  00:00:06   1.0033e+01     23          1.0070e+00   5.1191e-02   5.9292e-02   4.3766e+00   5.4918e+00   1.0000e-03
   40  00:00:06   9.0879e+00     24          1.0103e+00   6.4607e-02   6.5923e-02   4.1038e+00   4.8399e+00   1.0000e-03
   50  00:00:06   8.1398e+00     25          1.0120e+00   6.9854e-02   6.6607e-02   3.8008e+00   4.2010e+00   1.0000e-03
   60  00:00:06   7.2004e+00     26          1.0126e+00   6.8090e-02   6.0651e-02   3.4880e+00   3.5669e+00   1.0000e-03
   61  00:00:07   7.1277e+00     27  SN      1.0126e+00   6.7677e-02   5.9907e-02   3.4634e+00   3.5176e+00   1.0000e-03
   61  00:00:07   7.1277e+00     28  FP      1.0126e+00   6.7677e-02   5.9907e-02   3.4634e+00   3.5176e+00   1.0000e-03
   70  00:00:07   6.2764e+00     29          1.0123e+00   5.9969e-02   4.8123e-02   3.1700e+00   2.9355e+00   1.0000e-03
   80  00:00:07   5.3790e+00     30          1.0118e+00   4.6123e-02   2.9560e-02   2.8509e+00   2.3049e+00   1.0000e-03
   81  00:00:07   5.3602e+00     31  SN      1.0118e+00   4.5763e-02   2.9102e-02   2.8441e+00   2.2914e+00   1.0000e-03
   81  00:00:07   5.3602e+00     32  FP      1.0118e+00   4.5762e-02   2.9101e-02   2.8441e+00   2.2914e+00   1.0000e-03
   90  00:00:08   4.5423e+00     33          1.0149e+00   2.5311e-02   7.1105e-03   2.5521e+00   1.6650e+00   1.0000e-03
  100  00:00:08   4.0771e+00     34          1.0788e+00   4.4858e-03   4.2850e-05   2.3879e+00   1.2023e+00   1.0000e-03
  103  00:00:08   4.0688e+00     35  EP      1.1000e+00   3.5345e-03   2.0962e-05   2.3812e+00   1.1821e+00   1.0000e-03

 Run='sweepseps2.ep': Continue equilibria with varied omega at eps equal to 3.000000e-03.

    STEP   DAMPING               NORMS              COMPUTATION TIMES
  IT SIT     GAMMA     ||d||     ||f||     ||U||   F(x)  DF(x)  SOLVE
   0                          6.99e-18  9.99e+00    0.0    0.0    0.0

 STEP      TIME        ||U||  LABEL  TYPE            om         rho1         rho2          th1          th2          eps
    0  00:00:00   9.9885e+00      1  EP      1.0000e+00   4.2426e-02   1.2085e-01   3.9152e+00   5.7914e+00   3.0000e-03
..
  131  00:00:04   1.6794e+01     20  EP      7.0000e-01   3.5355e-03   6.9931e-06   5.4895e+00   1.0507e+01   3.0000e-03

 STEP      TIME        ||U||  LABEL  TYPE            om         rho1         rho2          th1          th2          eps
    0  00:00:04   9.9885e+00     21  EP      1.0000e+00   4.2426e-02   1.2085e-01   3.9152e+00   5.7914e+00   3.0000e-03
..
  118  00:00:09   4.0688e+00     38  EP      1.1000e+00   1.0605e-02   1.8872e-04   2.3812e+00   1.1822e+00   3.0000e-03

 Run='sweepseps3.ep': Continue equilibria with varied omega at eps equal to 5.000000e-03.

    STEP   DAMPING               NORMS              COMPUTATION TIMES
  IT SIT     GAMMA     ||d||     ||f||     ||U||   F(x)  DF(x)  SOLVE
   0                          7.27e-18  9.99e+00    0.0    0.0    0.0

 STEP      TIME        ||U||  LABEL  TYPE            om         rho1         rho2          th1          th2          eps
    0  00:00:00   9.9853e+00      1  EP      1.0000e+00   5.0820e-02   1.7340e-01   3.9144e+00   5.7878e+00   5.0000e-03
..
  137  00:00:04   1.6794e+01     20  EP      7.0000e-01   5.8926e-03   1.9426e-05   5.4895e+00   1.0507e+01   5.0000e-03

 STEP      TIME        ||U||  LABEL  TYPE            om         rho1         rho2          th1          th2          eps
    0  00:00:04   9.9853e+00     21  EP      1.0000e+00   5.0820e-02   1.7340e-01   3.9144e+00   5.7878e+00   5.0000e-03
..
  123  00:00:08   4.0689e+00     39  EP      1.1000e+00   1.7681e-02   5.2455e-04   2.3812e+00   1.1822e+00   5.0000e-03

 Run='sweepseps4.ep': Continue equilibria with varied omega at eps equal to 7.000000e-03.

    STEP   DAMPING               NORMS              COMPUTATION TIMES
  IT SIT     GAMMA     ||d||     ||f||     ||U||   F(x)  DF(x)  SOLVE
   0                          5.83e-15  9.98e+00    0.0    0.0    0.0

 STEP      TIME        ||U||  LABEL  TYPE            om         rho1         rho2          th1          th2          eps
    0  00:00:00   9.9834e+00      1  EP      1.0000e+00   5.7140e-02   2.1921e-01   3.9138e+00   5.7849e+00   7.0000e-03
..
  142  00:00:04   1.6794e+01     21  EP      7.0000e-01   8.2498e-03   3.8077e-05   5.4895e+00   1.0507e+01   7.0000e-03

 STEP      TIME        ||U||  LABEL  TYPE            om         rho1         rho2          th1          th2          eps
    0  00:00:04   9.9834e+00     22  EP      1.0000e+00   5.7140e-02   2.1921e-01   3.9138e+00   5.7849e+00   7.0000e-03
..
  129  00:00:10   4.0691e+00     40  EP      1.1000e+00   2.4766e-02   1.0291e-03   2.3813e+00   1.1823e+00   7.0000e-03

 Run='sweepseps5.ep': Continue equilibria with varied omega at eps equal to 1.000000e-02.

    STEP   DAMPING               NORMS              COMPUTATION TIMES
  IT SIT     GAMMA     ||d||     ||f||     ||U||   F(x)  DF(x)  SOLVE
   0                          6.81e-10  9.98e+00    0.0    0.0    0.0

 STEP      TIME        ||U||  LABEL  TYPE            om         rho1         rho2          th1          th2          eps
    0  00:00:00   9.9817e+00      1  EP      1.0000e+00   6.4627e-02   2.8042e-01   3.9131e+00   5.7812e+00   1.0000e-02
..
  149  00:00:06   1.6794e+01     21  EP      7.0000e-01   1.1786e-02   7.7718e-05   5.4895e+00   1.0507e+01   1.0000e-02

 STEP      TIME        ||U||  LABEL  TYPE            om         rho1         rho2          th1          th2          eps
    0  00:00:06   9.9817e+00     22  EP      1.0000e+00   6.4627e-02   2.8042e-01   3.9131e+00   5.7812e+00   1.0000e-02
..
  133  00:00:10   4.0695e+00     41  EP      1.1000e+00   3.5416e-02   2.1045e-03   2.3813e+00   1.1824e+00   1.0000e-02

Calculate FRC in physical domain at epsilon 1.000000e-03
Calculate FRC in physical domain at epsilon 3.000000e-03
Calculate FRC in physical domain at epsilon 5.000000e-03
Calculate FRC in physical domain at epsilon 7.000000e-03
Calculate FRC in physical domain at epsilon 1.000000e-02

FRCs on parametrisation space:

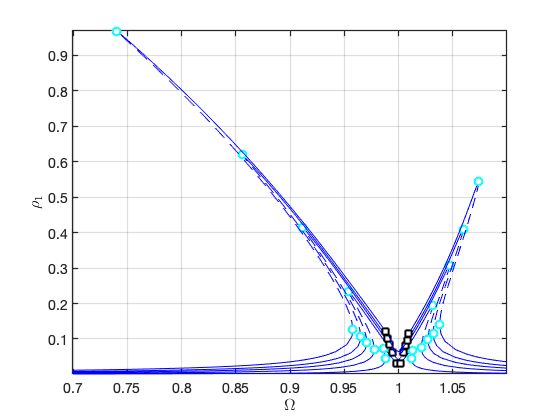
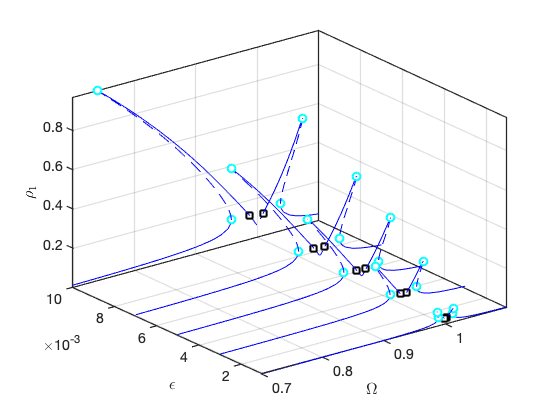
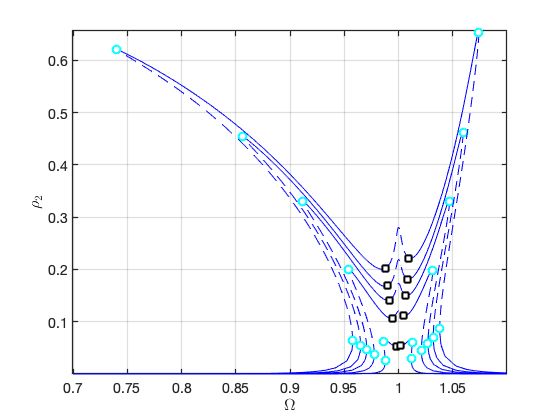
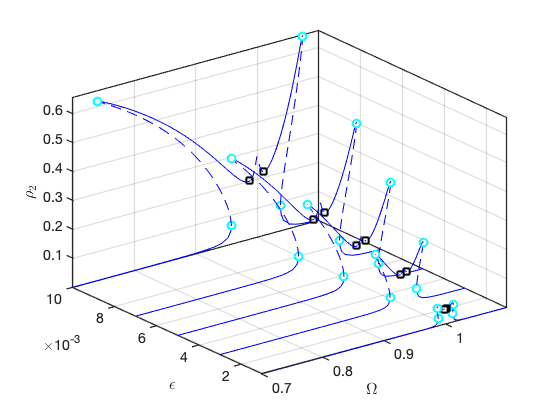
FRCs on physical DOF 1:

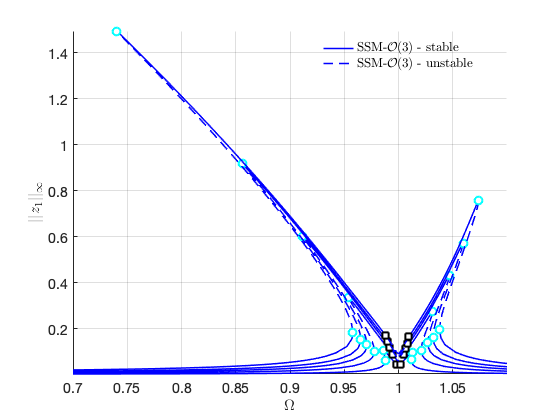
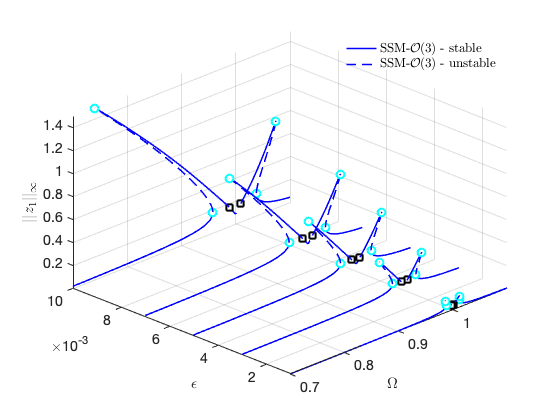
FRCs on physical DOF 2:

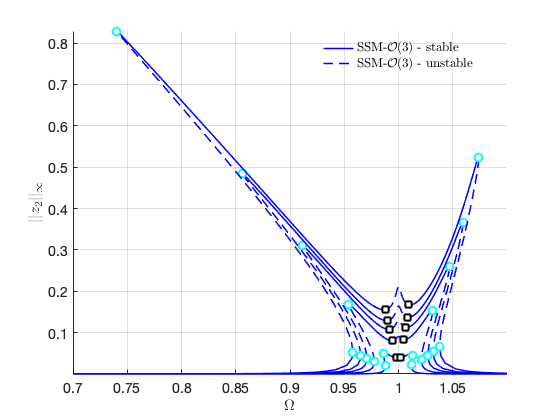
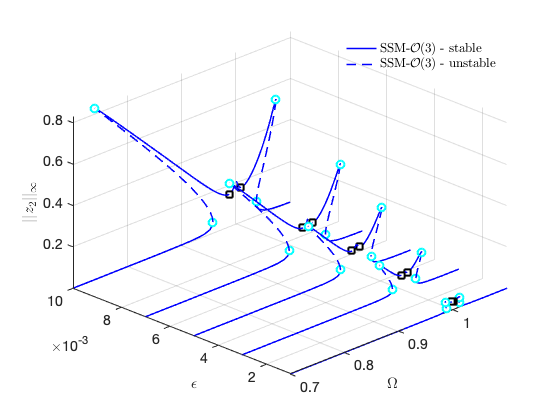
FRCs on physical DOF 3:

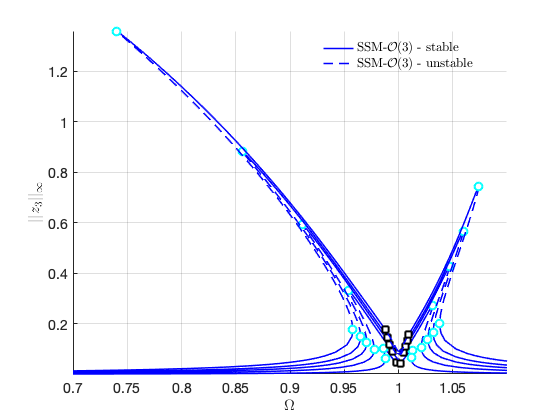
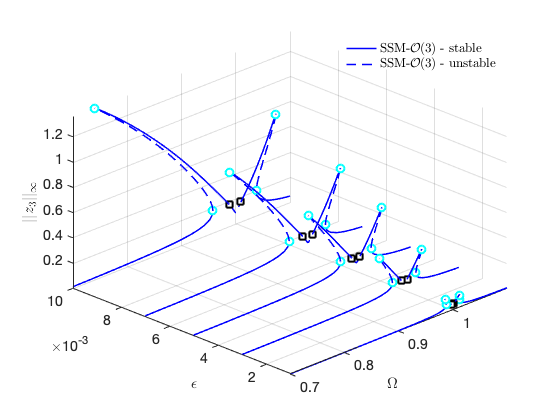
SSM_isol2ep:

continuation of equilibrium points from an initial solution*

set(S.contOptions, 'PtMX', 200, 'ItMX', 15, 'h_max', 0.5);    % continuation setting
FRC1 = S.SSM_isol2ep('isol_freq',resonant_modes,order,mFreq,'freq',freqRange,outdof);

The master subspace contains the following eigenvalues
 
lambda1 == - 0.0025 + 1i
 
lambda2 == (-0.0025) - 1i
 
lambda3 == - 0.005 + 2i
 
lambda4 == (-0.005) - 2i
 
sigma_out = 0
sigma_in = 1
Manifold computation time at order 2 = 00:00:00
Estimated memory usage at order  2 = 1.25E-02 MB
Manifold computation time at order 3 = 00:00:00
Estimated memory usage at order  3 = 2.04E-02 MB

Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the value of the function tolerance, and
the problem appears regular as measured by the gradient.


 Run='isol_freq.ep': Continue equilibria along primary branch.

    STEP   DAMPING               NORMS              COMPUTATION TIMES
  IT SIT     GAMMA     ||d||     ||f||     ||U||   F(x)  DF(x)  SOLVE
   0                          6.81e-10  9.98e+00    0.0    0.0    0.0

 STEP      TIME        ||U||  LABEL  TYPE            om         rho1         rho2          th1          th2          eps
    0  00:00:00   9.9817e+00      1  EP      1.0000e+00   6.4627e-02   2.8042e-01   3.9131e+00   5.7812e+00   1.0000e-02
    8  00:00:00   7.8756e+00      2  HB      9.8785e-01   1.2167e-01   2.0189e-01   2.7123e+00   4.7565e+00   1.0000e-02
   10  00:00:00   7.8607e+00      3          9.8581e-01   1.3071e-01   2.0058e-01   2.6964e+00   4.7535e+00   1.0000e-02
   20  00:00:01   7.9165e+00      4          9.7414e-01   1.8020e-01   2.1142e-01   2.6838e+00   4.8069e+00   1.0000e-02
   30  00:00:01   1.0622e+01      5          7.8212e-01   8.5499e-01   5.7517e-01   3.4976e+00   6.5200e+00   1.0000e-02
   33  00:00:01   1.2015e+01      6  SN      7.4027e-01   9.6886e-01   6.2061e-01   3.9382e+00   7.4030e+00   1.0000e-02
   33  00:00:01   1.2016e+01      7  FP      7.4027e-01   9.6885e-01   6.2061e-01   3.9382e+00   7.4031e+00   1.0000e-02
   40  00:00:01   1.5088e+01      8          8.9664e-01   4.5826e-01   3.4531e-01   4.9416e+00   9.3952e+00   1.0000e-02
   43  00:00:02   1.6420e+01      9  FP      9.5793e-01   1.2662e-01   6.3998e-02   5.3826e+00   1.0242e+01   1.0000e-02
   43  00:00:02   1.6423e+01     10  SN      9.5793e-01   1.2584e-01   6.3212e-02   5.3836e+00   1.0244e+01   1.0000e-02
   50  00:00:02   1.6722e+01     11          9.1392e-01   4.1481e-02   3.3542e-03   5.4682e+00   1.0444e+01   1.0000e-02
   60  00:00:02   1.6788e+01     12          7.8029e-01   1.6096e-02   1.9792e-04   5.4864e+00   1.0498e+01   1.0000e-02
   63  00:00:02   1.6794e+01     13  EP      7.0000e-01   1.1786e-02   7.7718e-05   5.4895e+00   1.0507e+01   1.0000e-02

 STEP      TIME        ||U||  LABEL  TYPE            om         rho1         rho2          th1          th2          eps
    0  00:00:02   9.9817e+00     14  EP      1.0000e+00   6.4627e-02   2.8042e-01   3.9131e+00   5.7812e+00   1.0000e-02
    9  00:00:03   1.2066e+01     15  HB      1.0096e+00   1.1508e-01   2.2170e-01   5.0685e+00   6.7837e+00   1.0000e-02
   10  00:00:03   1.2086e+01     16          1.0108e+00   1.2130e-01   2.2108e-01   5.0845e+00   6.7893e+00   1.0000e-02
   20  00:00:03   1.2065e+01     17          1.0182e+00   1.6033e-01   2.3278e-01   5.1099e+00   6.7498e+00   1.0000e-02
   30  00:00:04   1.0124e+01     18          1.0640e+00   4.6440e-01   5.5392e-01   4.4942e+00   5.4213e+00   1.0000e-02
   35  00:00:04   8.1347e+00     19  SN      1.0741e+00   5.4396e-01   6.5319e-01   3.8231e+00   4.0736e+00   1.0000e-02
   35  00:00:04   8.1346e+00     20  FP      1.0741e+00   5.4396e-01   6.5319e-01   3.8230e+00   4.0735e+00   1.0000e-02
   40  00:00:04   5.5219e+00     21          1.0564e+00   3.5217e-01   3.6393e-01   2.9304e+00   2.2991e+00   1.0000e-02
   43  00:00:05   4.3623e+00     22  FP      1.0379e+00   1.4332e-01   9.0076e-02   2.5024e+00   1.4652e+00   1.0000e-02
   43  00:00:05   4.3493e+00     23  SN      1.0380e+00   1.4009e-01   8.6228e-02   2.4974e+00   1.4549e+00   1.0000e-02
   50  00:00:05   4.0732e+00     24          1.0885e+00   4.0081e-02   3.0453e-03   2.3847e+00   1.1924e+00   1.0000e-02
   52  00:00:05   4.0695e+00     25  EP      1.1000e+00   3.5416e-02   2.1045e-03   2.3813e+00   1.1824e+00   1.0000e-02

Response on parametrisation space:

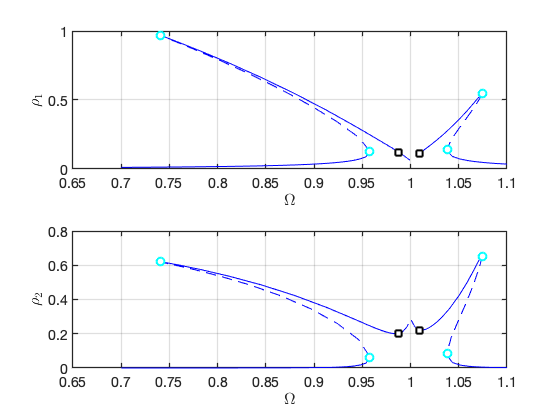
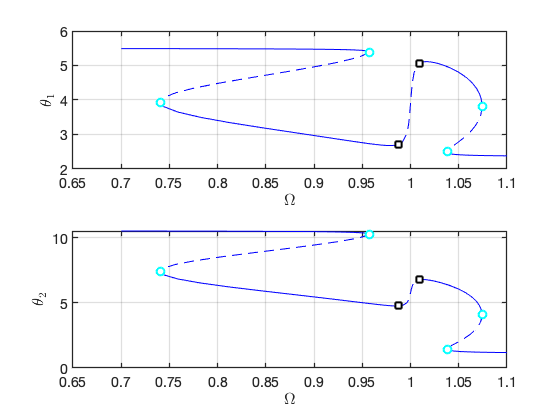
FRCs on physical space:

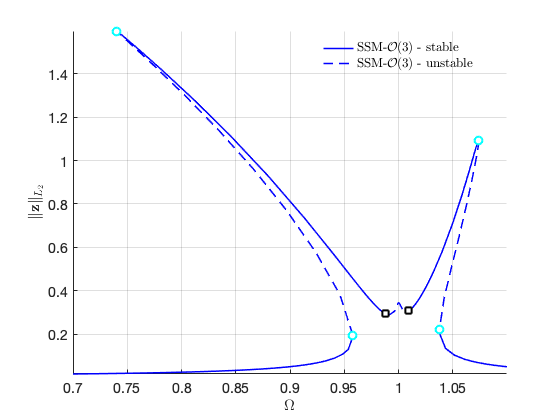
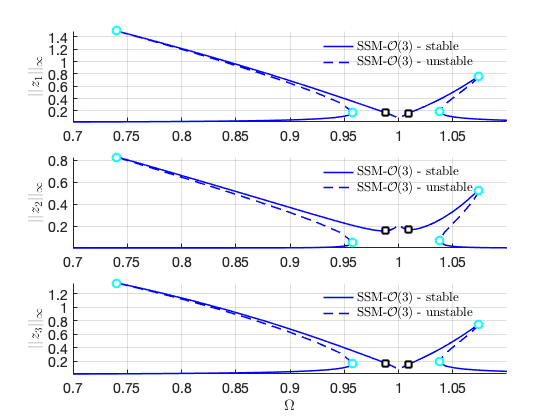
The above continuation is performed with varied $\Omega$ , as indicated by the keyword 'freq'. On the other hand, we may vary the forcing amplitude $\epsilon$ instead of $\Omega$

epsRange = [0.01 5]*epsilon;
FRC2     = S.SSM_isol2ep('isol_amp',resonant_modes,order,mFreq,'amp',epsRange,outdof);

The master subspace contains the following eigenvalues
 
lambda1 == - 0.0025 + 1i
 
lambda2 == (-0.0025) - 1i
 
lambda3 == - 0.005 + 2i
 
lambda4 == (-0.005) - 2i
 
sigma_out = 0
sigma_in = 1
Manifold computation time at order 2 = 00:00:00
Estimated memory usage at order  2 = 1.25E-02 MB
Manifold computation time at order 3 = 00:00:00
Estimated memory usage at order  3 = 2.04E-02 MB

Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the value of the function tolerance, and
the problem appears regular as measured by the gradient.


 Run='isol_amp.ep': Continue equilibria along primary branch.

    STEP   DAMPING               NORMS              COMPUTATION TIMES
  IT SIT     GAMMA     ||d||     ||f||     ||U||   F(x)  DF(x)  SOLVE
   0                          6.81e-10  9.93e+00    0.0    0.0    0.0

 STEP      TIME        ||U||  LABEL  TYPE           eps         rho1         rho2          th1          th2           om
    0  00:00:00   9.9315e+00      1  EP      1.0000e-02   6.4627e-02   2.8042e-01   3.9131e+00   5.7812e+00   1.0000e+00
    4  00:00:00   9.9483e+00      2  HB      6.9311e-04   2.4500e-02   4.0295e-02   3.9177e+00   5.7995e+00   1.0000e+00
    8  00:00:00   9.9667e+00      3  EP      9.9158e-05   9.5999e-03   6.1868e-03   3.9232e+00   5.8117e+00   1.0000e+00

 STEP      TIME        ||U||  LABEL  TYPE           eps         rho1         rho2          th1          th2           om
    0  00:00:00   9.9315e+00      4  EP      1.0000e-02   6.4627e-02   2.8042e-01   3.9131e+00   5.7812e+00   1.0000e+00
    4  00:00:00   9.9538e+00      5  EP      5.0000e-02   1.1169e-01   8.3723e-01   3.9075e+00   5.7494e+00   1.0000e+00

Continuation in Epsilon:

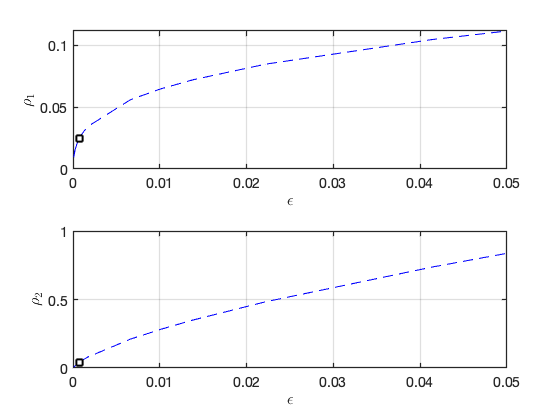
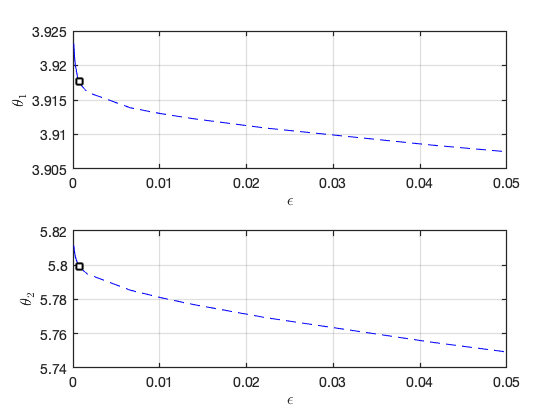
Result in physical coordinates:

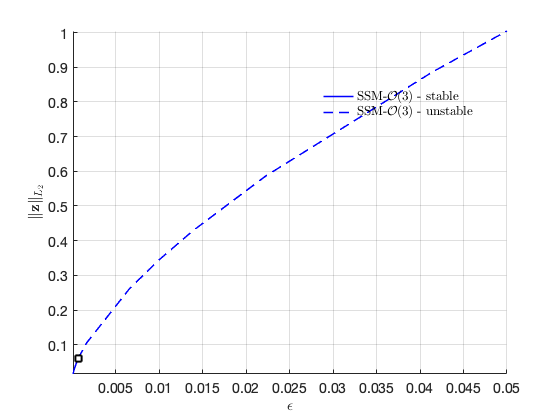
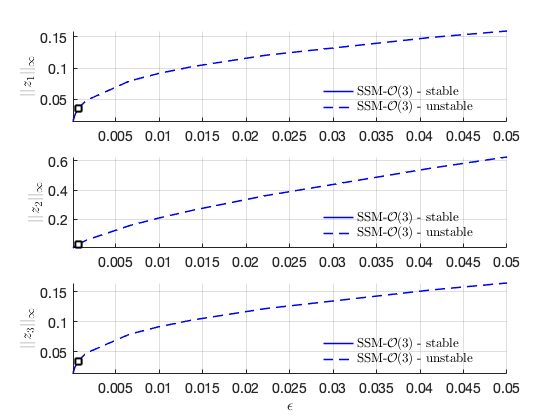
SSM_ep2ep:

We can also directly perform continuation of equilibrium points from saved solutions to obtain these results.

FRC3 = S.SSM_ep2ep('ep','isol_freq',1,'amp',epsRange,outdof);

 Run='ep.ep': Continue equilibria from label 1 of run isol_freq.

    STEP   DAMPING               NORMS              COMPUTATION TIMES
  IT SIT     GAMMA     ||d||     ||f||     ||U||   F(x)  DF(x)  SOLVE
   0                          6.81e-10  9.93e+00    0.0    0.0    0.0

 STEP      TIME        ||U||  LABEL  TYPE           eps         rho1         rho2          th1          th2           om
    0  00:00:00   9.9315e+00      1  EP      1.0000e-02   6.4627e-02   2.8042e-01   3.9131e+00   5.7812e+00   1.0000e+00
    4  00:00:00   9.9483e+00      2  HB      6.9311e-04   2.4500e-02   4.0295e-02   3.9177e+00   5.7995e+00   1.0000e+00
    8  00:00:00   9.9667e+00      3  EP      9.9158e-05   9.5999e-03   6.1868e-03   3.9232e+00   5.8117e+00   1.0000e+00

 STEP      TIME        ||U||  LABEL  TYPE           eps         rho1         rho2          th1          th2           om
    0  00:00:00   9.9315e+00      4  EP      1.0000e-02   6.4627e-02   2.8042e-01   3.9131e+00   5.7812e+00   1.0000e+00
    4  00:00:00   9.9538e+00      5  EP      5.0000e-02   1.1169e-01   8.3723e-01   3.9075e+00   5.7494e+00   1.0000e+00

Continuation in Epsilon:

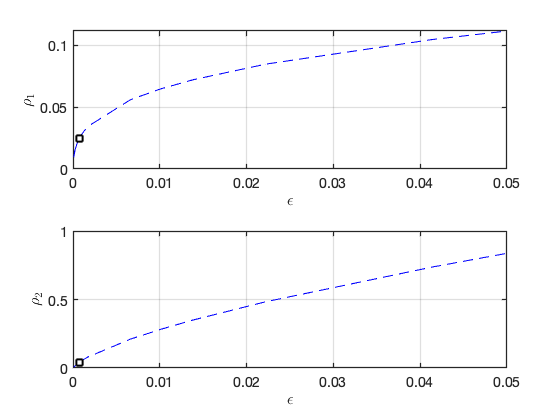
Result in physical coordinates:

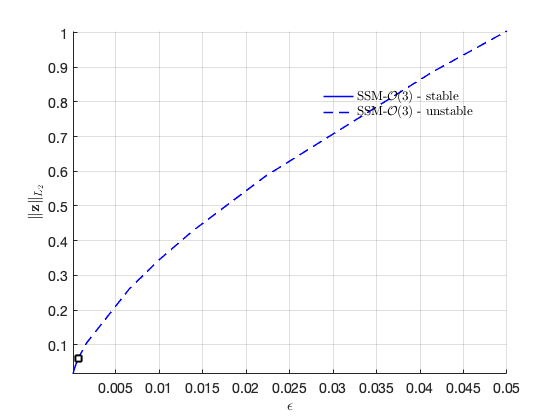
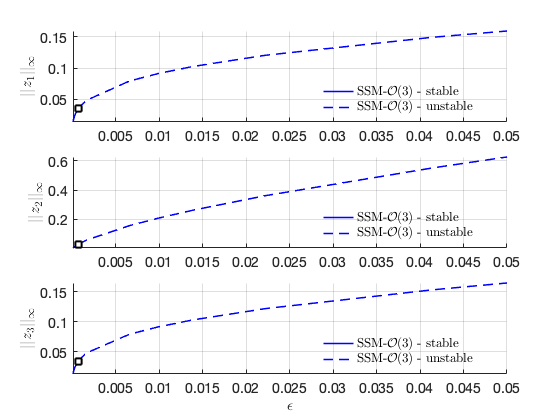
SSM_ep2SN:

This allows for the continuation of Saddle-Node bifurcation equilibrium points. We wish to investigate how the critical response amplitude for which the saddle node bifurcation occurs changes, if the forcing parameters are changed.

SNlab = 6; % or you use bd=coco_bd_read('isol.ep'); SNlabs=coco_bd_labs(bd, 'SN') to find it
FRC4  = S.SSM_ep2SN('SN','isol_freq',SNlab,{freqRange,epsRange},outdof);

 Run='SN.ep': Continue saddle-node equilibria from label 6 of run isol_freq.

    STEP   DAMPING               NORMS              COMPUTATION TIMES
  IT SIT     GAMMA     ||d||     ||f||     ||U||   F(x)  DF(x)  SOLVE
   0                          6.53e-08  1.21e+01    0.0    0.0    0.0

 STEP      TIME        ||U||  LABEL  TYPE            om          eps         rho1         rho2          th1          th2
    0  00:00:00   1.2057e+01      1  EP      7.4027e-01   1.0000e-02   9.6886e-01   6.2061e-01   3.9382e+00   7.4030e+00
    2  00:00:00   1.2070e+01      2  EP      7.0000e-01   1.0844e-02   1.0741e+00   6.6133e-01   3.9363e+00   7.4005e+00

 STEP      TIME        ||U||  LABEL  TYPE            om          eps         rho1         rho2          th1          th2
    0  00:00:00   1.2057e+01      3  EP      7.4027e-01   1.0000e-02   9.6886e-01   6.2061e-01   3.9382e+00   7.4030e+00
   10  00:00:00   1.2262e+01      4          9.6408e-01   2.4302e-03   1.8548e-01   1.6133e-01   4.0509e+00   7.5683e+00
   20  00:00:01   1.3141e+01      5          9.8844e-01   8.1460e-04   5.8432e-02   4.8542e-02   4.3882e+00   8.0995e+00
   23  00:00:01   1.4071e+01      6  FP      9.9089e-01   6.1250e-04   3.9680e-02   2.8009e-02   4.7065e+00   8.6811e+00
   30  00:00:01   1.6298e+01      7          9.6875e-01   5.6798e-03   9.6261e-02   4.9710e-02   5.3419e+00   1.0140e+01
   40  00:00:02   1.6594e+01      8          9.3843e-01   2.0528e-02   1.7646e-01   8.5083e-02   5.4212e+00   1.0338e+01
   46  00:00:02   1.6708e+01      9  EP      9.0055e-01   5.0000e-02   2.6602e-01   1.1994e-01   5.4516e+00   1.0414e+01

Bifurcations occur for the following forcing parameters:

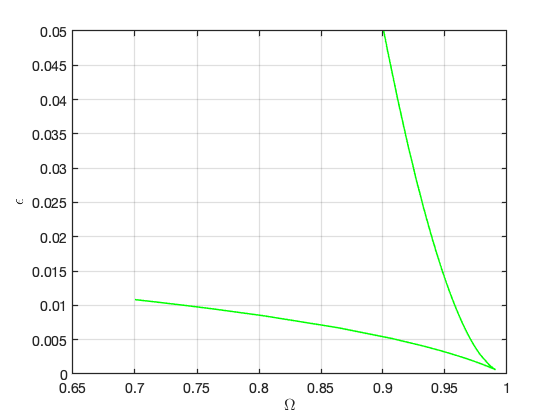
Bifurcations in parametrisation space:

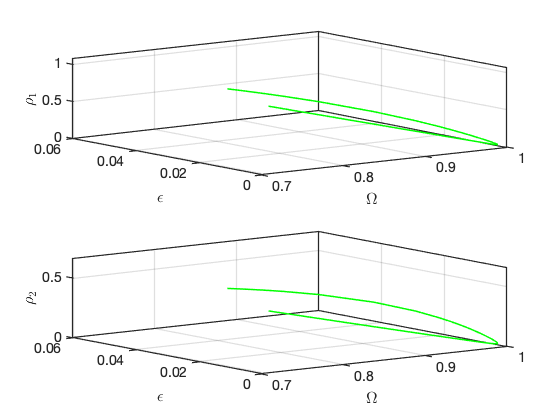
Bifurcations in physical space:

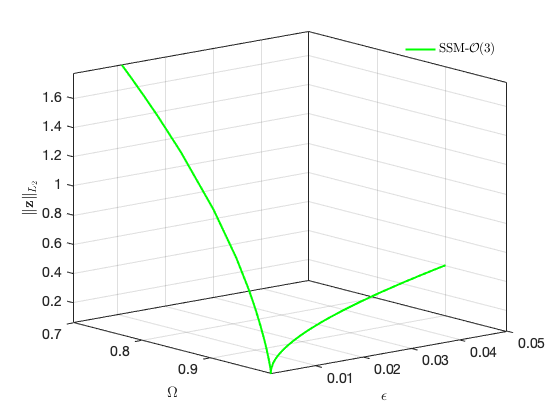
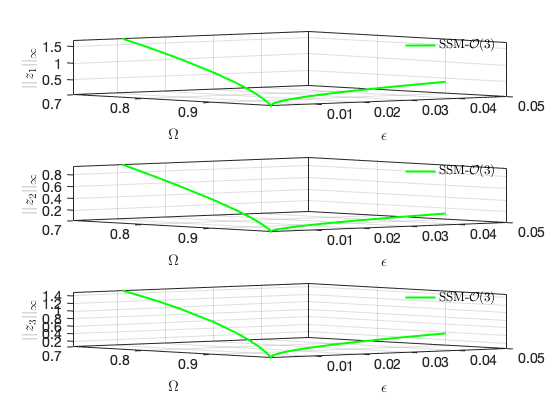
SSM_ep2HB:

This routine can be used for the continuation of Hopf bifurcation equilibrium points. We wish to investigate how the critical response amplitude for which the hopf bifurcation occurs changes, if the forcing parameters are changed.

HBlab = 2; % or you use HBlabs = coco_bd_labs(bd, 'HB') to find it
FRC5  = S.SSM_ep2HB('HB','isol_freq',HBlab,{freqRange,epsRange},outdof);

 Run='HB.ep': Continue Hopf equilibria from label 2 of run isol_freq.

    STEP   DAMPING               NORMS              COMPUTATION TIMES
  IT SIT     GAMMA     ||d||     ||f||     ||U||   F(x)  DF(x)  SOLVE
   0                          1.00e-08  7.94e+00    0.0    0.0    0.0

 STEP      TIME        ||U||  LABEL  TYPE            om          eps         rho1         rho2          th1          th2
    0  00:00:00   7.9388e+00      1  EP      9.8785e-01   1.0000e-02   1.2167e-01   2.0189e-01   2.7123e+00   4.7565e+00
    9  00:00:00   7.4546e+00      2  EP      9.6773e-01   5.0000e-02   2.8553e-01   4.2955e-01   2.4981e+00   4.4542e+00

 STEP      TIME        ||U||  LABEL  TYPE            om          eps         rho1         rho2          th1          th2
    0  00:00:00   7.9388e+00      3  EP      9.8785e-01   1.0000e-02   1.2167e-01   2.0189e-01   2.7123e+00   4.7565e+00
   10  00:00:01   9.9192e+00      4          9.9922e-01   7.3688e-04   2.5660e-02   4.2247e-02   3.7632e+00   5.7907e+00
   20  00:00:01   1.0529e+01      5          1.0021e+00   1.1010e-03   3.3329e-02   5.7490e-02   4.3285e+00   5.9319e+00
   30  00:00:02   1.2441e+01      6          1.0143e+00   2.3854e-02   1.7741e-01   3.5793e-01   5.2038e+00   6.9725e+00
   35  00:00:02   1.2643e+01      7  EP      1.0194e+00   5.0000e-02   2.5347e-01   5.3965e-01   5.2805e+00   7.0810e+00

Bifurcations occur for the following forcing parameters:

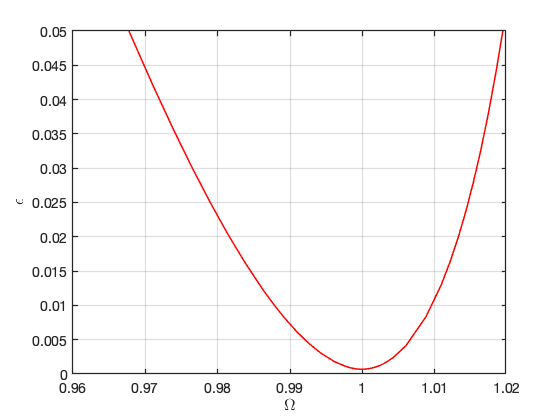
Bifurcations in parametrisation space:

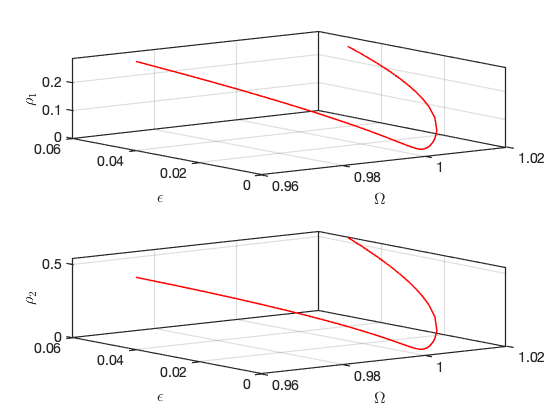
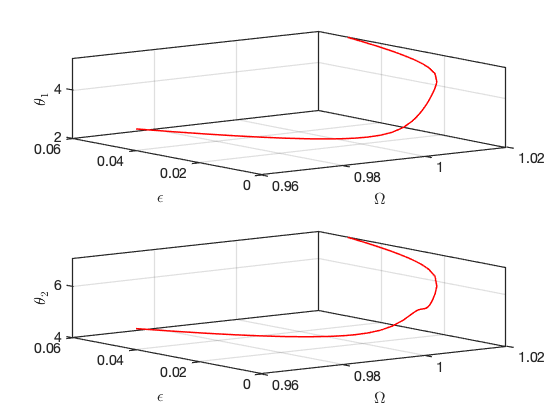
Bifurcations in physical space:

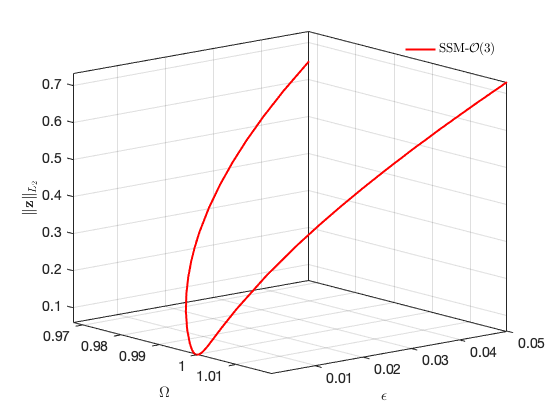
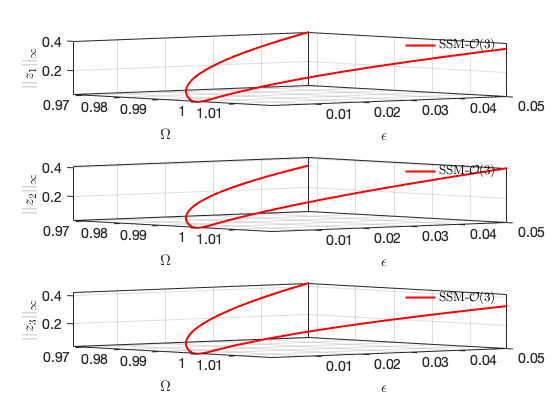
SSM_BP2ep:

We now consider the primary resonance of the second mode and demonstrate how to use SSM_BP2ep to switch to the secondary branch. We use Cartesian coordinates.

fext   = [0;1];
coeffs = [fext fext]/2;
DS.add_forcing(coeffs, kappas, epsilon);
set(S.FRCOptions,'coordinates','cartesian')

mFreq     = [1/2 1];
freqRange = [0.9 1.1]*imag(D(3));
set(S.contOptions, 'PtMX', 150);    % continuation setting

FRC6 = S.SSM_isol2ep('isol_2ndfreq',resonant_modes,order,mFreq,...
    'freq',freqRange,outdof);

The master subspace contains the following eigenvalues
 
lambda1 == - 0.0025 + 1i
 
lambda2 == (-0.0025) - 1i
 
lambda3 == - 0.005 + 2i
 
lambda4 == (-0.005) - 2i
 
sigma_out = 0
sigma_in = 1
Manifold computation time at order 2 = 00:00:00
Estimated memory usage at order  2 = 1.25E-02 MB
Manifold computation time at order 3 = 00:00:00
Estimated memory usage at order  3 = 2.04E-02 MB

Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the value of the function tolerance, and
the problem appears regular as measured by the gradient.


 Run='isol_2ndfreq.ep': Continue equilibria along primary branch.

    STEP   DAMPING               NORMS              COMPUTATION TIMES
  IT SIT     GAMMA     ||d||     ||f||     ||U||   F(x)  DF(x)  SOLVE
   0                          1.51e-10  2.98e+00    0.0    0.0    0.0

 STEP      TIME        ||U||  LABEL  TYPE            om         Rez1         Rez2         Imz1         Imz2          eps
    0  00:00:00   2.9835e+00      1  EP      2.0000e+00   8.6965e-10   6.0050e-01  -8.6965e-10  -3.0025e-01   1.0000e-02
   10  00:00:00   2.9470e+00      2          1.9974e+00  4.8808e-114   5.9398e-01 -1.6988e-113   1.2378e-02   1.0000e-02
   20  00:00:00   2.8815e+00      3          1.9938e+00  4.8722e-286   3.8160e-01 -1.5394e-286   1.7556e-01   1.0000e-02
   30  00:00:01   2.8138e+00      4          1.9817e+00  1.9763e-323   1.1842e-01 -3.4585e-323   1.3205e-01   1.0000e-02
   34  00:00:01   2.7821e+00      5  SN      1.9649e+00  1.9763e-323   5.3903e-02 -3.4585e-323   7.7911e-02   1.0000e-02
   34  00:00:01   2.7821e+00      6  BP      1.9649e+00  1.9763e-323   5.3903e-02 -3.4585e-323   7.7911e-02   1.0000e-02
   40  00:00:02   2.7342e+00      7          1.9327e+00  1.9763e-323   2.5502e-02 -3.4585e-323   4.2750e-02   1.0000e-02
   49  00:00:02   2.5457e+00      8  EP      1.8000e+00 -4.9407e-324   7.8768e-03 -4.9407e-324   1.4816e-02   1.0000e-02

 STEP      TIME        ||U||  LABEL  TYPE            om         Rez1         Rez2         Imz1         Imz2          eps
    0  00:00:02   2.9835e+00      9  EP      2.0000e+00   8.6965e-10   6.0050e-01  -8.6965e-10  -3.0025e-01   1.0000e-02
   10  00:00:03   2.9542e+00     10          2.0026e+00  2.5221e-113   3.4648e-01 -1.6786e-114  -4.8262e-01   1.0000e-02
   20  00:00:03   2.8988e+00     11          2.0062e+00  2.5663e-286   8.8507e-02 -6.3550e-286  -4.1061e-01   1.0000e-02
   30  00:00:03   2.8653e+00     12          2.0182e+00  4.9407e-324  -3.4593e-02  2.4703e-323  -1.7397e-01   1.0000e-02
   34  00:00:04   2.8810e+00     13  SN      2.0349e+00  4.9407e-324  -3.0063e-02  2.4703e-323  -9.0281e-02   1.0000e-02
   34  00:00:04   2.8810e+00     14  BP      2.0349e+00  4.9407e-324  -3.0063e-02  2.4703e-323  -9.0281e-02   1.0000e-02
   40  00:00:04   2.9244e+00     15          2.0672e+00  4.9407e-324  -1.8900e-02  2.4703e-323  -4.6051e-02   1.0000e-02
   49  00:00:05   3.1114e+00     16  EP      2.2000e+00  4.9407e-324  -7.1266e-03 -4.9407e-324  -1.5191e-02   1.0000e-02

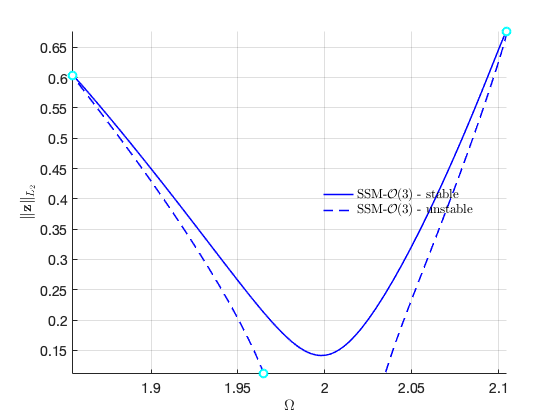
FRCs on parametrisation space:

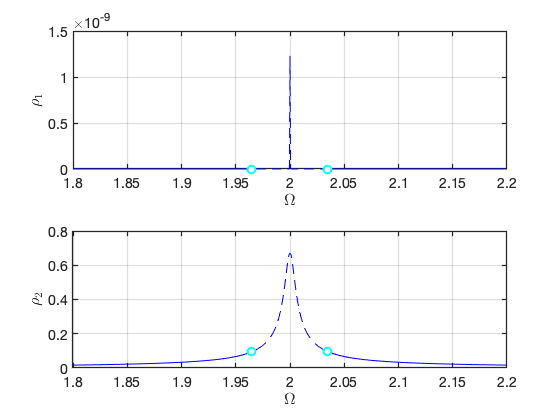
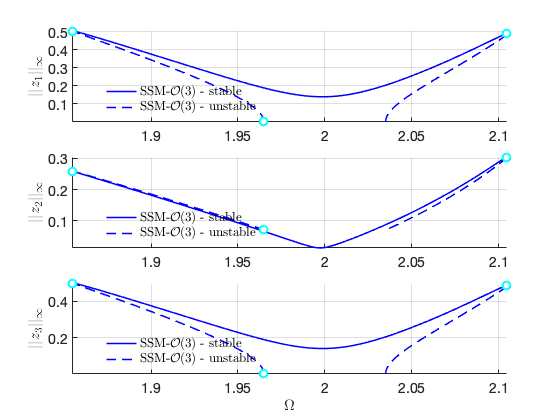
FRCs on physical space:

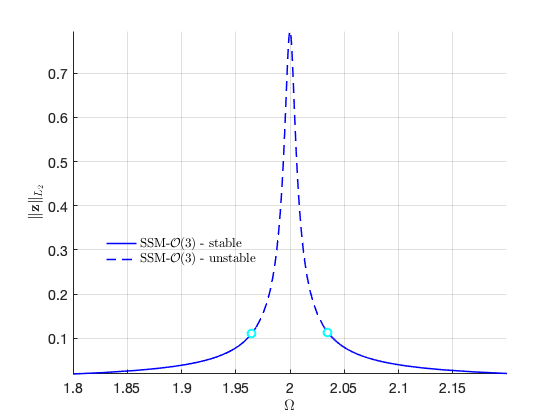
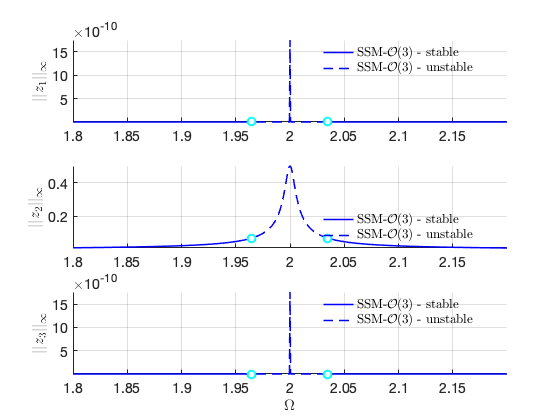
Continuation along the secondary branch:

BPlab = 6;
set(S.contOptions,'bi_direct',false)
FRC6_BP = S.SSM_BP2ep('BPep','isol_2ndfreq',BPlab,'freq',freqRange,outdof);

 Run='BPep.ep': Continue equilibria along secondary branch from label 6 of run isol_2ndfreq.

 STEP      TIME        ||U||  LABEL  TYPE            om         Rez1         Rez2         Imz1         Imz2          eps
    0  00:00:00   2.7821e+00      1  EP      1.9649e+00  1.9763e-323   5.3903e-02 -3.4585e-323   7.7911e-02   1.0000e-02
    1  00:00:00   2.7821e+00      2  BP      1.9649e+00  -1.7779e-09   5.3903e-02  -1.0581e-09   7.7911e-02   1.0000e-02
    1  00:00:00   2.7821e+00      3  SN      1.9649e+00  -2.1056e-08   5.3903e-02  -1.5793e-08   7.7911e-02   1.0000e-02
    1  00:00:00   2.7822e+00      4  FP      1.9650e+00  -1.3633e-03   5.3634e-02  -9.4722e-04   7.7819e-02   1.0000e-02
   35  00:00:01   2.7004e+00      8  FP      1.8551e+00  -3.4978e-01   2.6141e-01   1.5599e-03  -1.1855e-01   1.0000e-02
   35  00:00:01   2.7004e+00      9  SN      1.8551e+00  -3.4978e-01   2.6141e-01   1.5603e-03  -1.1855e-01   1.0000e-02
  113  00:00:03   3.0667e+00     18  FP      2.1048e+00   3.1129e-03   3.3672e-01   3.4955e-01  -1.9106e-01   1.0000e-02
  113  00:00:03   3.0667e+00     19  SN      2.1048e+00   3.1133e-03   3.3672e-01   3.4955e-01  -1.9106e-01   1.0000e-02
  148  00:00:04   2.8810e+00     23  BP      2.0349e+00  -3.0517e-09  -3.0063e-02  -3.5567e-09  -9.0282e-02   1.0000e-02
  148  00:00:04   2.8810e+00     24  FP      2.0349e+00  -8.8576e-07  -3.0063e-02  -1.1805e-06  -9.0282e-02   1.0000e-02
  150  00:00:04   2.8817e+00     25  EP      2.0353e+00  -9.8826e-03  -2.9951e-02  -1.3230e-02  -9.1735e-02   1.0000e-02

Oscillatory system with 2:1 internal resonance

Contents

Setup model

SSM computation

SSM_epSweeps:

FRCs on parametrisation space:

FRCs on physical DOF 1:

FRCs on physical DOF 2:

FRCs on physical DOF 3:

SSM_isol2ep:

Response on parametrisation space:

FRCs on physical space:

Continuation in Epsilon:

Result in physical coordinates:

SSM_ep2ep:

Continuation in Epsilon:

Result in physical coordinates:

SSM_ep2SN:

Bifurcations occur for the following forcing parameters:

Bifurcations in parametrisation space:

Bifurcations in physical space:

SSM_ep2HB:

Bifurcations occur for the following forcing parameters:

Bifurcations in parametrisation space:

Bifurcations in physical space:

SSM_BP2ep:

FRCs on parametrisation space:

FRCs on physical space:

FRCs on parametrisation space:

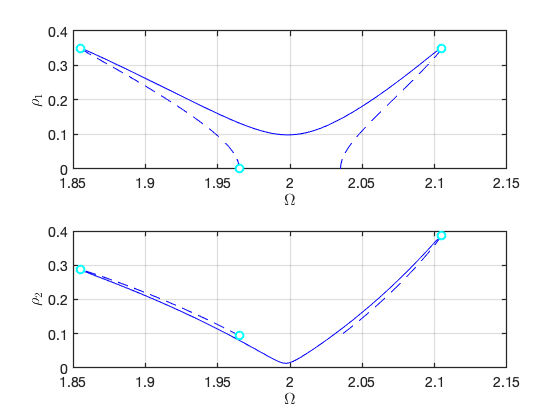
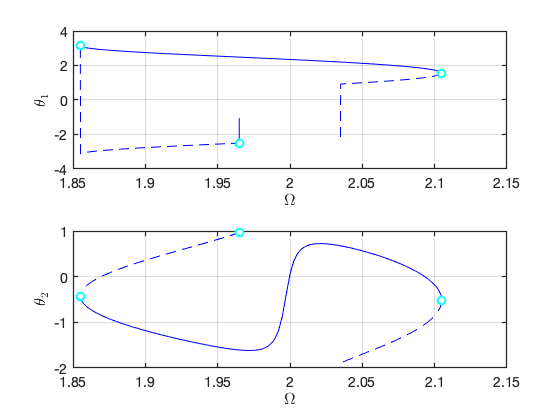
FRCs on physical space: