On the Non-intrusive computation of SSMs

Contents

Algorithmic use

To couple SSMTool with generic FEM solvers, which do not provide an explicit description of the nonlinear forces, we provide the functionality of computing SSMs nonintrusively (for systems with up to cubic nonlinearities).

We assume that the nonlinear function is provided as a function handle with a single input vector $\mathbf{f}_{nl}(\mathbf{z})$ , with $\mathbf{z} = (\mathbf{x, \dot{x}})^T$ .

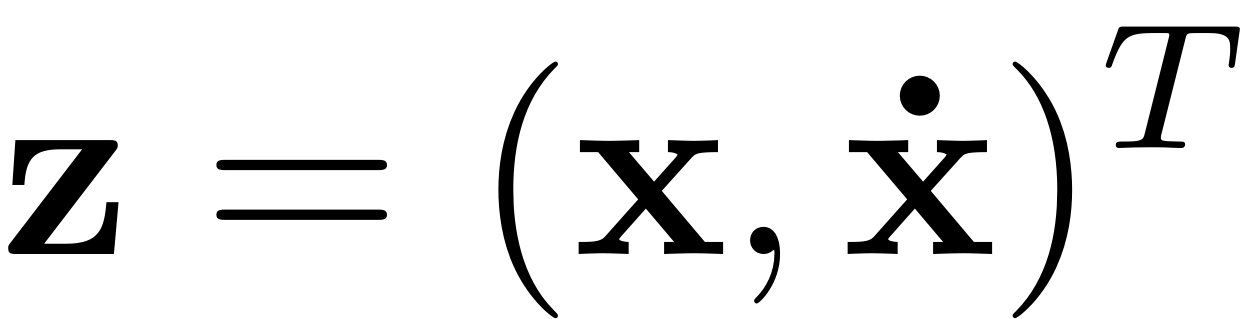If the nonlinearity is provided as a function handle with this characteristic, it can be passed to the SSM algorithm via

set(DS,'fnl_non',fnl_non);
        

For the non-autonomous computation the function handle for the Jacobian needs to be provided as well. It is given as

$D_\mathbf{z}\mathbf{F} (\mathbf{z}) = \sum_{j>2} j \mathbf{F}_j ( \mathbf{z} , \underbrace{\mathbf{z, \cdots , z}}_{j-1 \textrm{ times}})$

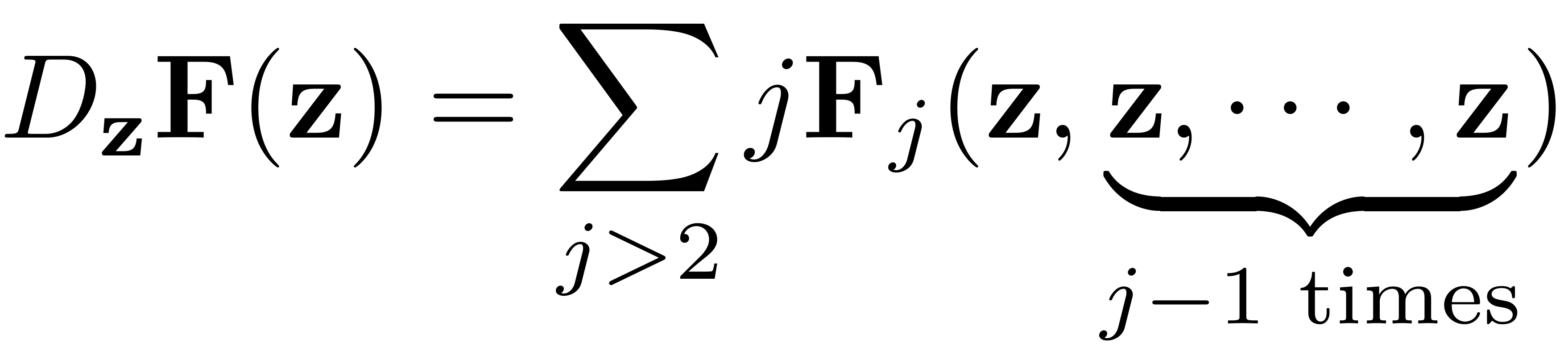
Consequently this function handle is passed to the dynamical system class via

set(DS,'dfnl_non',dfnl_non);
        

If the input dynamical system is first order, the input function handles are passed as

set(DS,'F_non',F_non);
set(DS,'dF_non',dF_non);
        

The following settings should be made, to run the code in its semi-intrusive version:

set(DS.Options,'Intrusion','non')
        

Examples

To get familiar with setting up such a function handle please refer to the following examples, which we provide:

Using this routine we also may combine SSMTool with FEM software such as COMSOL The following examples use a model in COMSOL, without having explicit access to the model nonlinearities:

Mathematical Details

Mathematical details can be found in the related publication:

Published with MATLAB® R2023a