On the Semi-intrusive computation of SSMs
Contents
Algorithmic use
To reduce memory requirements for handling the non-linear forces, we provide and algorithm for computing SSMs in a semi-intrusive manner. The method does not require full intrusion into a code to construct the nonlinear tensors as it does deal with function handles, very much like a non-intrusive algorithm would.
We assume that the function handle for evaluating the order
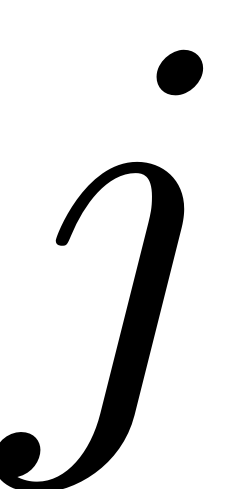 nonlinearity takes
nonlinearity takes
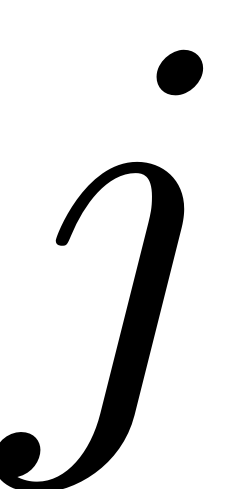 separate input vectors.
separate input vectors.
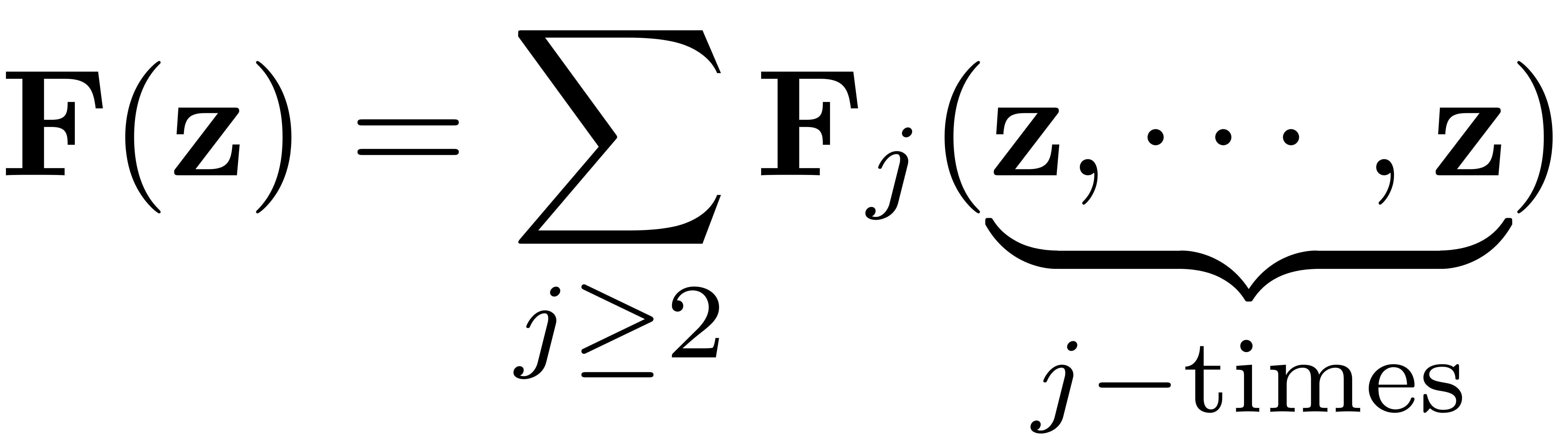
If the nonlinearity is provided as a function handle with this characteristic, it can be passed to the SSM algorithm via
set(DS,'fnl_semi',fnl);
For the non-autonomous computation the function handle for the Jacobian needs to be provided as well. It is given as
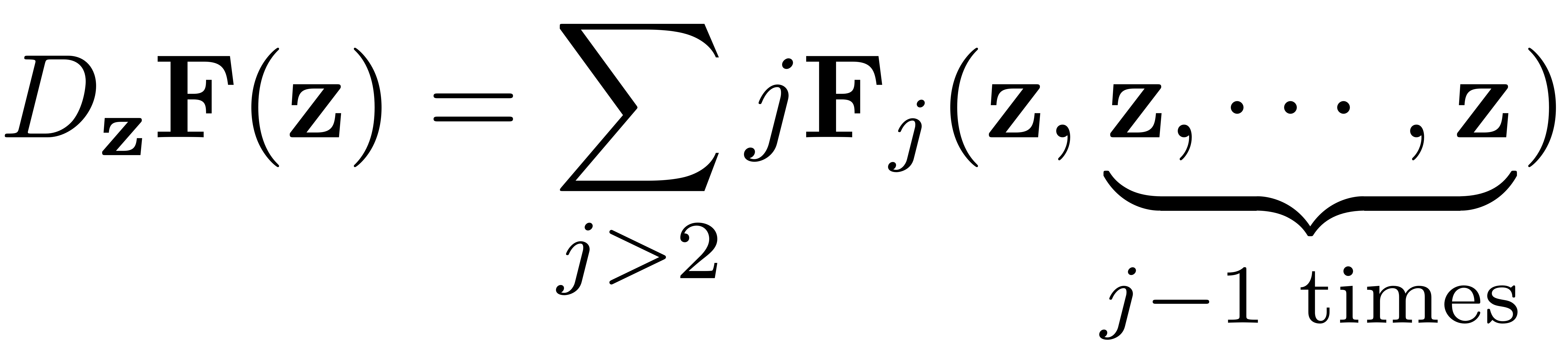
Consequently this function handle is passed to the dynamical system class via
set(DS,'dfnl_semi',dfnl);
If the input dynamical system is first order, the input function handles are passed as
set(DS,'F_semi',F_semi); set(DS,'dF_semi',dF_semi);
The following settings should be made, to run the code in its semi-intrusive version:
set(DS.Options,'Intrusion','semi')
If the function is symmetric with respect to its input handles, the following parameter can be set for an additional speedup:
set(DS.Options, 'F_semi_sym', true) % by default an asymmetric function handle is assumed
Examples
To get familiar with how to the semi-intrusive routine refer to the examples:
- Semi-Intrusive computation of the van Karman Shell example.
- Semi-Intrusive computation of the NACA Wing example.
Mathematical Details
We note that the nonlinear functions effectively evaluate a series of homogeneous polynomials. Thus their composition with the autonomous SSM parametrisation can be written as
It is now straightforward to collect terms corresponding to the same
multi-indices. We then find the nonlinear contribution of
 to the cohomological equation to be
to the cohomological equation to be
![$$ [\ \mathbf{F} \circ \mathbf{W} ]_{\mathbf{m}} = \sum_{j=2}^m
\big(
\sum_{ \mathbf{m}_1, \cdots , \mathbf{m}_j \in \mathbf{N}^M}
\mathbf{F}_j (\mathbf{W}_{\mathbf{m}_1} , \cdots ,\mathbf{W}_{\mathbf{m}_j} )
\big)
\Bigr|_{ \sum_{i=1}^j \mathbf{m}_i = \mathbf{m}}
\\\ \ \
=
\sum_{j=2}^m
\big(
\sum_{ \mathbf{m}_1 \leq \cdots \leq \mathbf{m}_j \in \mathbf{N}^M}
\sigma [\mathbf{m}_1, \cdots , \mathbf{m}_j]
\mathbf{F}_j (\mathbf{W}_{\mathbf{m}_1} , \cdots ,\mathbf{W}_{\mathbf{m}_j} )
\big)
\Bigr|_{ \sum_{i=1}^j \mathbf{m}_i = \mathbf{m}} $$](SemiIntrusion_eq01993812740548891117-Rescaled.png)
In the last line the symmetry of the function handle is used. For
each combination of multi-indices that sum up to a multi-index
 the function is evaluated only once and afterwards multiplied by the
number of possible permutations, here denoted by
the function is evaluated only once and afterwards multiplied by the
number of possible permutations, here denoted by
![$\sigma [\mathbf{m}_1, \cdots , \mathbf{m}_j]$](SemiIntrusion_eq16347338019077272349-Rescaled.png) . Permutations of identical multi-indices are not counted. The
evaluation of the non-autonomous contribution can be computed
as follows. As the Jacobian is directly evaluated along the
non-autonomous SSM parametrisation we avoid a direct construction of
the matrix itself by using the first entry of the function handle.
If for some reason a full representation of the Jacobian matrix is
desired, its
. Permutations of identical multi-indices are not counted. The
evaluation of the non-autonomous contribution can be computed
as follows. As the Jacobian is directly evaluated along the
non-autonomous SSM parametrisation we avoid a direct construction of
the matrix itself by using the first entry of the function handle.
If for some reason a full representation of the Jacobian matrix is
desired, its
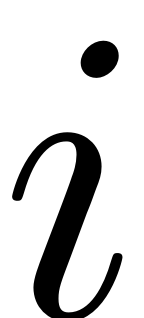 -th column may be obtained by setting
-th column may be obtained by setting
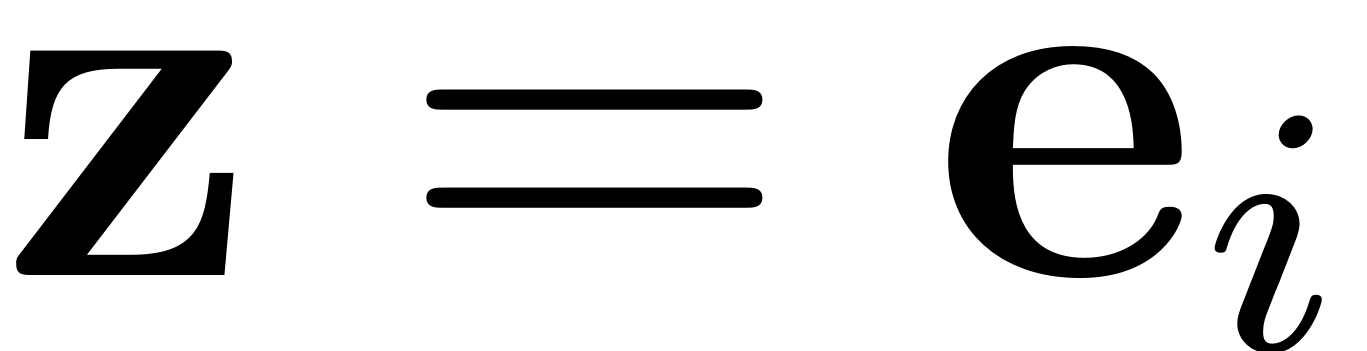 in the first entry. We can now follow an argument analogous to the
autonomous computation which allows to pull out the sums of the
function evaluation and group terms corresponding to the same
multi-index. For a given harmonic
in the first entry. We can now follow an argument analogous to the
autonomous computation which allows to pull out the sums of the
function evaluation and group terms corresponding to the same
multi-index. For a given harmonic
 the application of this Jacobian to the non-autonomous
parametrisation thus results in a term of the form
the application of this Jacobian to the non-autonomous
parametrisation thus results in a term of the form
![$$ [ ( \textrm{D}_\mathbf{z} \mathbf{F} \circ \mathbf{W}) \mathbf{X}
]_{\mathbf{m}} =
\sum_{ \mathbf{k,l} \in \mathbf{N}^M, \ \mathbf{k+l=m}} \textrm{D}_\mathbf{z} \mathbf{F} \circ \mathbf{W}\Bigr|_{\mathbf{m}}
\mathbf{X}_ {\mathbf{l}, \mathbf{\kappa}}
\\ \ \ \
=
\sum_{j=2}^m j
\sum_{ \mathbf{k,l}\in \mathbf{N}^M, \ \mathbf{k+l=m}}
(
\sum_{ \mathbf{k}_1 \leq \cdots \leq \mathbf{k}_{j-1} \in \mathbf{N}^M}
\sigma [\mathbf{k}_1, \cdots , \mathbf{k}_{j-1}] \
\mathbf{F}_j (\mathbf{X}_{\mathbf{l},\mathbf{\kappa}} ,\mathbf{W}_{\mathbf{k}_1} , \cdots ,\mathbf{W}_{\mathbf{k}_{j-1}} )
)
\Bigr|_{ \sum_{i=1}^{j-1} \mathbf{k}_i = \mathbf{k}} $$](SemiIntrusion_eq17350587505660427418-Rescaled.png)
