Residual

function [ r, drdqdd,drdqd,drdq, c0] = residual(obj, q, qd, qdd, t)

This function computes the residual needed for time integration of second-order system

$\mathbf{M}\ddot{\mathbf{q}} + \mathbf{C}\dot{\mathbf{q}} + \mathbf{F}(\mathbf{q}) =\mathbf{F}_{\textrm{ext}}(t)$

where we use the residual defined as

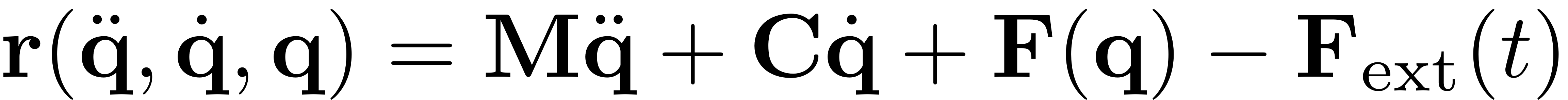
$\mathbf{r}(\ddot{\mathbf{q}},\dot{\mathbf{q}},\mathbf{q}) = \mathbf{M}\ddot{\mathbf{q}} + \mathbf{C}\dot{\mathbf{q}} + \mathbf{F}(\mathbf{q}) - \mathbf{F}_{\textrm{ext}}(t)$

assert(obj.order == 2, ' residual can only be computed for second-order systems')

F_elastic = obj.K * q + obj.compute_fnl(q,qd);
F_external =  obj.compute_fext(t,q);
F_inertial = obj.M * qdd;
F_damping = obj.C * qd;

r = F_inertial + F_damping + F_elastic - F_external ;
drdqdd = obj.M;
drdqd = obj.C + obj.compute_dfnldxd(q,qd);
drdq = obj.K + obj.compute_dfnldx(q,qd);

We use the following measure to compare the norm of the residual $\mathbf{r}$

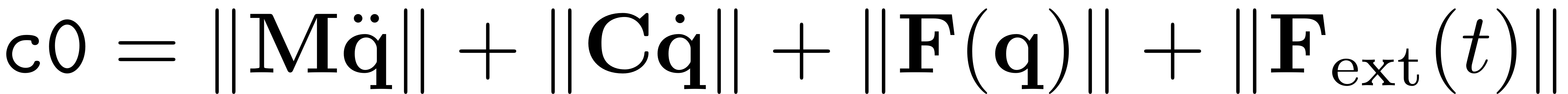
$\texttt{c0} = \|\mathbf{M}\ddot{\mathbf{q}}\| + \|\mathbf{C}\dot{\mathbf{q}}\| + \|\mathbf{F}(\mathbf{q})\| + \|\mathbf{F}_{\textrm{ext}}(t)\|$

c0 = norm(F_inertial) + norm(F_damping) + norm(F_elastic) + norm(F_external);

end